
| 公务员 | 教师 | 合计 | |
| 同意延迟退休 | 40 | n | 70 |
| 不同意延迟退休 | m | 20 | p |
| 合计 | 50 | 50 | 100 |
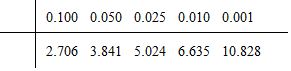
分析 (Ⅰ)根据题中提供的数据,得到m=10,n=30,p=30.从而求出K2=$\frac{100}{21}≈4.762>3.841$,从而有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)公务员有4人同意,1人不同电,教师有3人同意,2人不同意,从两个职业人群中各抽取巧人,同意延迟退休的人数X的取值为1,2,3,4,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)根据题中提供的数据,得到:
$\left\{\begin{array}{l}{40+m=50}\\{n+20=50}\\{70+p=100}\end{array}\right.$,
解得m=10,n=30,p=30.
K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{100(40×20-30×10)^{2}}{50×50×70×30}$=$\frac{100}{21}≈4.762>3.841$,
∴有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)公务员有4人同意,1人不同电,教师有3人同意,2人不同意,
从两个职业人群中各抽取巧人,同意延迟退休的人数X的取值为1,2,3,4,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{5}^{2}{C}_{5}^{2}}$=$\frac{1}{25}$,
P(X=2)=$\frac{{C}_{4}^{1}{C}_{2}^{1}{C}_{3}^{1}+{C}_{4}^{2}{C}_{2}^{2}}{{C}_{5}^{2}{C}_{5}^{2}}$=$\frac{3}{10}$,
P(X=4)=$\frac{{C}_{4}^{2}{C}_{3}^{2}}{{C}_{5}^{2}{C}_{5}^{2}}$=$\frac{9}{50}$,
P(X=3)=1-$\frac{1}{25}-\frac{3}{10}-\frac{9}{50}$=$\frac{12}{25}$,
∴X的分布列为:
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{25}$ | $\frac{3}{10}$ | $\frac{12}{25}$ | $\frac{9}{50}$ |
点评 本题考查K2的求法及应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
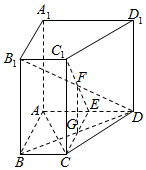 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com