
| A. | a30,a1 | B. | a1,a30 | C. | a8,a30 | D. | a8,a7 |
分析 把给出的数列的通项公式变形,把an看作n的函数,作出相应的图象,由图象分析得到答案.
解答 解:an=$\frac{n-\sqrt{51}}{n-\sqrt{52}}$,
∴an=$\frac{n-\sqrt{52}-\sqrt{51}+\sqrt{52}}{n-\sqrt{52}}$=1+$\frac{\sqrt{52}-\sqrt{51}}{n-\sqrt{52}}$,
当1≤n≤7时,an单调递减,且a7<1为最小;
当8≤n≤30时,an单调递减,且a8>1为最大.
∴这个数列的前30项中最大项和最小项分别是a8,a7.
故答案选:D.
点评 本题考查了利用函数的单调性求数列的最大值与最小值,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
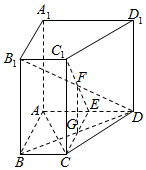 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com