
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
���� ���ڢڣ�����f��0��=0���ó�a1•sin����1��+a2•sin����2��+��+an•sin����n��=0��Ҫ�жϺ���Ϊ�溯����ֻ����֤f��-x��+f��x��=0��
���ڢۣ�����f��$\frac{��}{2}$��=0���ó�-a1•cos����1��-a2•cos����2��+��-an•cos����n��=0��Ҫ�жϺ���Ϊż������ֻ����֤f��-x��-f��x��=0��
���ڢ٣��ɢ�֪����f��x��Ϊ�溯�����ɢ�֪����Ϊż�������Ӷ�f��x��=0��
���ڢܣ���f2��0��+f2��$\frac{��}{2}$����0ʱ����f��x1��=f��x2��=0���ã�sinx1-sinx2����a1cos��1+��+ancos��n��+��cosx1-cosx2����a1sin��1+��+ansin��n��=0���ʿɵý��ۣ�
��� �⣺�ߺ���f��x��=a1sin��x+a1��+a2sin��x+a2��+��+ansin��x+an����
����ai��aj��i=1��2������n��n��N*��n��2��Ϊ��֪ʵ������x��R��
���ڢڣ���f��0��=0����f��0��=a1•sin����1��+a2•sin����2��+��+an•sin����n��=0��
f��-x��+f��x��=a1•sin��-x+��1��+a2•sin��-x+��2��+��+an•sin��-x+��n��+a1•sin��x+��1��+a2•sin��x+��2��+��+an•sin��x+��n��
=2cosx[a1•sin��1+a2•sin��2+��+an•sin��n]=0��
�ຯ��f��x��Ϊ�溯�����ʢ���ȷ��
���ڢۣ���f��$\frac{��}{2}$��=0����f��$\frac{��}{2}$��=a1•sin��$\frac{��}{2}$+��1��+a2•sin��$\frac{��}{2}$+��2��+��+an•sin��$\frac{��}{2}$+��n��
=-a1•cos����1��-a2•cos����2��-��-an•cos����n��=0��
��f��-x��-f��x��=a1•sin��-x+��1��+a2•sin��-x+��2��+��+an•sin��-x+��n��
-a1•sin��x+��1��-a2•sin��x+��2��-��-an•sin��x+��n��=2sinx[a1•cos��1+a2•cos��2+��+an•cos��n]=0��
�ຯ��f��x��Ϊż�������ʢ���ȷ��
���ڢ٣���f��0��=f��$\frac{��}{2}$��=0������f��x��Ϊ�溯����ҲΪż������
��f��x��=0������ʵ��x��������ʢ���ȷ��
���ڢܣ���f2��0��+f2��$\frac{��}{2}$����0ʱ����f��x1��=f��x2��=0��
��f��x1��=a1•sin��x1+��1��+a2•sin��x1+��2��+��+an•sin��x1+��n��
=f��x2��=a1•sin��x2+��1��+a2•sin��x2+��2��+��+an•sin��x2+��n��=0��
�ࣨsinx1-sinx2����a1cos��1+��+ancos��n��+��cosx1-cosx2����a1sin��1+��+ansin��n��=0��
��sinx1-sinx2 =0���ɵ�x1-x2=k�У�k��Z�����ʢ���ȷ��
��ѡ��A��
���� ����Ŀ��������������Ǻ������ۺϣ���Ҫ�������Ǻ����Ļ������¶������Ǻ��������ʣ�����Ĺؼ���һһ�жϣ������е��⣮


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {3} | B�� | {2��3} | C�� | {1��2��3} | D�� | [2��3] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=|sinx| | B�� | y=|cosx| | C�� | y=sin2x | D�� | y=cos2x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
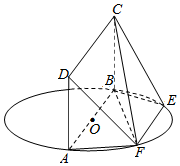 ��ͼ��ABΪԲO��ֱ������E��F��ԲO�ϣ�AB��EF������ABCD����ƽ���ԲO���ڵ�ƽ�滥�ഹֱ����֪AB=2��EF=1��
��ͼ��ABΪԲO��ֱ������E��F��ԲO�ϣ�AB��EF������ABCD����ƽ���ԲO���ڵ�ƽ�滥�ഹֱ����֪AB=2��EF=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����� | 10�� | 9�� | 8�� |
| �� �� | 0.12 | 0.18 | 0.28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a30��a1 | B�� | a1��a30 | C�� | a8��a30 | D�� | a8��a7 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com