
 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{8}{25}$ | D. | $\frac{1}{3}$ |
分析 由条件便可分别以BC,BA为x轴,y轴,建立平面直角坐标系,并根据条件设AB=4,从而BC=3,这样即可求出A,B,C,D四点的坐标,并设E(x,y),从而可以由$\overrightarrow{CE}=λ\overrightarrow{BD}$可得$\left\{\begin{array}{l}{x-3=3λ}\\{y=4λ}\end{array}\right.$(1),而根据$\overrightarrow{AE}⊥\overrightarrow{CE}$可得到x(x-3)+y(y-4)=0(2),这样由(1)(2)联立便可求出λ的值.
解答 解:根据条件,分别以BC,BA所在直线为x,y轴,建立如图所示平面直角坐标系,设AB=4,则: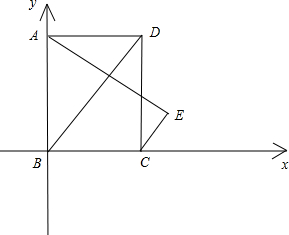
B(0,0),A(0,4),C(3,0),D(3,4);$\overrightarrow{BD}=(3,4)$;
设E(x,y),$\overrightarrow{AE}=(x,y-4),\overrightarrow{CE}=(x-3,y)$,$\overrightarrow{BD}=(3,4)$;
∴由$\overrightarrow{CE}=λ\overrightarrow{BD}$得,(x-3,y)=λ(3,4);
∴$\left\{\begin{array}{l}{x-3=3λ}\\{y=4λ}\end{array}\right.$(1);
∵$\overrightarrow{AE}⊥\overrightarrow{CE}$;
∴$\overrightarrow{AE}•\overrightarrow{CE}=0$;
即x(x-3)+y(y-4)=0,带入(1)得:
(3λ+3)3λ+4λ(4λ-4)=0;
解得$λ=\frac{7}{25}$,或λ=0(舍去).
故选:B.
点评 考查通过建立平面直角坐标系,利用坐标解决向量问题的方法,能求平面上点的坐标,根据点的坐标可求向量的坐标,向量坐标的数乘运算,以及向量垂直的充要条件,向量数量积的坐标运算.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了引导学生树立正确的消费观,抽取了某校部分学生的每周消费情况,绘制成频率分布直方图如图,则图中实数a的值为( )
为了引导学生树立正确的消费观,抽取了某校部分学生的每周消费情况,绘制成频率分布直方图如图,则图中实数a的值为( )| A. | 0.04 | B. | 0.05 | C. | 0.06 | D. | 0.07 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{12},0)$ | B. | $(\frac{π}{3},-\frac{1}{4})$ | C. | $(\frac{π}{3},0)$ | D. | $(\frac{7π}{24},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 67 | B. | 68 | C. | 69 | D. | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com