
过原点的直线交双曲线  于P,Q两点,现将坐标平面沿直线y= -x折成直二面角,则折后PQ长度的最小值等于
于P,Q两点,现将坐标平面沿直线y= -x折成直二面角,则折后PQ长度的最小值等于
A. | B.4 | C. | D. |
B
解析试题分析:∵双曲线 是等轴双曲线,以直线y=±x为渐近线
是等轴双曲线,以直线y=±x为渐近线
∴将双曲线按逆时针方向旋转45°角,可得双曲线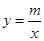 的图象
的图象
∵双曲线 的顶点(
的顶点( ,0),逆时针方向旋转45°
,0),逆时针方向旋转45°
变为点( ,
, )
)
∴点( ,
, )在
)在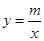 的图象上,可得m=
的图象上,可得m= ,
,
即双曲线按逆时针方向旋转45°角,得到双曲线 的图象
的图象
问题转化为:过原点的直线交双曲线 于P、Q两点
于P、Q两点
将坐标平面沿直线y轴折成直二面角,求折后线段PQ的长度的最小值
设P(t, )(t>0),过点P作PM⊥y轴于M,连结MQ,
)(t>0),过点P作PM⊥y轴于M,连结MQ,
可得M(0, ),Q(-t,-
),Q(-t,- ),
),
|MQ|= =
= ,在折叠后的图形中,Rt△PMQ中,|PM|=t,
,在折叠后的图形中,Rt△PMQ中,|PM|=t,
得|PQ|2=|PM|2+|MQ|2= ≥
≥ =16,
=16,
当且仅当t2=4,即t=2时等号成立,
∴当t=2时,即P坐标为(2, )时,|PQ|的最小值为
)时,|PQ|的最小值为 =4.
=4.
综上所述,折后线段PQ的长度的最小值等于4,故选B.
考点:两点间的距离公式、面面垂直的性质、勾股定理,基本不等式求最值,逻辑推理能力,运算能力,转化与化归思想,数形结合思想


科目:高中数学 来源: 题型:解答题
已知圆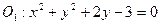 内一定点
内一定点 ,
, 为圆上的两不同动点.
为圆上的两不同动点.
(1)若 两点关于过定点
两点关于过定点 的直线
的直线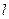 对称,求直线
对称,求直线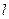 的方程.
的方程.
(2)若圆 的圆心
的圆心 与点
与点 关于直线
关于直线 对称,圆
对称,圆 与圆
与圆 交于
交于 两点,且
两点,且 ,求圆
,求圆 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知抛物线的顶点在原点,焦点在x轴的正半轴上,若抛物线的准线与双曲线5x2-y2= 20的两条渐近线围成的三角形的面积等于 ,则抛物线的方程为
,则抛物线的方程为
| A.y2=4x | B.y2=8x | C.x2=4y | D.x2=8y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com