
分析 (1)设动点G的坐标(x,y),求出直线EG的斜率,直线FG的斜率,利用已知条件求解即可.
(2)由圆O与直线l相切,知m2=k2+1,联立直线与椭圆,得(1+2k2)x2+4kmx+2m2-2=0,由直线l与椭圆交于两个不同点,得到k2>0,利用$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{2}{3}$时,求出k,即可求△AOB的面积.
解答 解:(1)已知E(0,1),F(0,-1),设动点G的坐标(x,y),
∵动点G满足:直线EG与直线FG的斜率之积为-$\frac{1}{2}$,
∴$\frac{y-1}{x}×\frac{y+1}{x}$=-$\frac{1}{2}$,即$\frac{{x}^{2}}{2}+{y}^{2}=1(x≠0)$.
(2)∵圆O与直线l相切,∴$\frac{|m|}{\sqrt{{k}^{2}+1}}$=1,即m2=k2+1,
联立直线与椭圆,消去y,得(1+2k2)x2+4kmx+2m2-2=0,
∵直线l与椭圆交于两个不同点,∴△=(4km)2-4(1+2k2)(2m2-2)>0,
∴k2>0,
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1•x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,
∴y1y2=(kx1+m)(kx2+m)=$\frac{1-{k}^{2}}{1+2{k}^{2}}$,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{1+{k}^{2}}{1+2{k}^{2}}$=$\frac{2}{3}$
∴k2=1,
∴S△ABO=$\frac{1}{2}\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{\frac{2({k}^{4}+{k}^{2})}{4({k}^{4}+{k}^{2})+1}}$=$\frac{2}{3}$.
点评 本题考查直线与椭圆方程的综合应用,椭圆方程的求法,考查向量知识的运用,考查分析问题解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
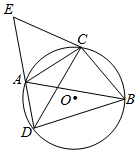 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示.
一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
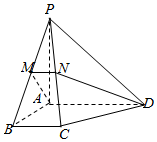 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
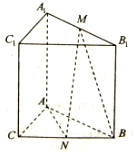 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,点M和N分别为A1B1和BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,点M和N分别为A1B1和BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
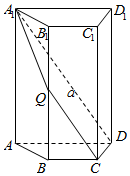 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
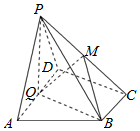 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在地平线上 | B. | 仰角为30° | C. | 仰角为45° | D. | 仰角为60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com