
已知A、B、C是直线l上不同的三点,O是l外一点,向量 满足:
满足:
 记y=f(x).
记y=f(x).
(1)求函数y=f(x)的解析式:
(2)若对任意 不等式|a-lnx|-ln[f '(x)-3x]>0恒成立,求实数a的取值范围:
不等式|a-lnx|-ln[f '(x)-3x]>0恒成立,求实数a的取值范围:
(3)若关于x的方程f(x)=2x+b在[0,1]上恰有两个不同的实根,求实数b的取值范围.
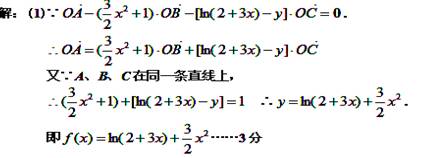
(2)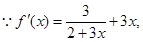 ∴原不等式为
∴原不等式为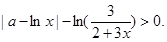
得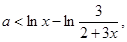 或
或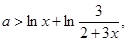 ①……4分
①……4分
设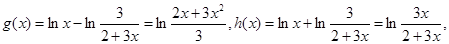
依题意知a<g(x)或a>h(x)在x∈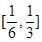 上恒成立,
上恒成立,
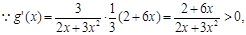
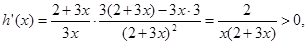
∴g(x)与h(x)在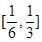 上都是增函数,要使不等式①成立,
上都是增函数,要使不等式①成立,
当且仅当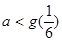 或
或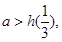 ∴
∴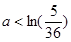 ,或
,或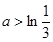 .……8分
.……8分
(3)方程f(x)=2x+b即为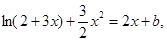
变形为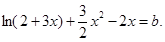
令j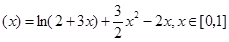 ,
,
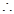 j
j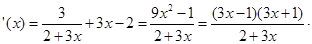 ……10分
……10分
列表写出 x,j'(x),j(x)在[0,1]上的变化情况:
|
x |
0 |
(0, |
|
( |
1 |
|
j'(x) |
|
小于0 |
0 |
大于0 |
|
|
j(x) |
ln2 |
单调递减 |
取极小值
|
单调递增 |
|
……12分
显然j(x)在[0,1]上的极小值也即为它的最小值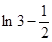 .
.
现在比较ln2与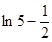 的大小;
的大小;
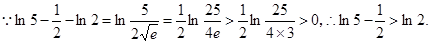
∴要使原方程在[0,1]上恰有两个不同的实根,必须使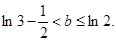
即实数b的取值范围为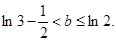 ……14分
……14分
【解析】略


科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| OA |
| 3 |
| 2 |
| OB |
| OC |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| OA |
| 3 |
| 2 |
| OB |
| OC |
| 0 |
| 1 |
| 6 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| 3 |
| 2+3x |
| OC |
| 0 |
| 1 |
| 6 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com