
| A. | 2013 | B. | 2014 | C. | 4026 | D. | 4028 |
分析 根据抽象函数的表达式,令x1=x2=0,可求得f(0)=2014;再利用单调性的定义证明函数f(x)在R上为单调递增函数,f(x1)+f(-x1)=4028,从而可求M+N.
解答 解:∵对于任意的x1,x2∈[-2015,2015],都有f(x1+x2)=f(x1)+f(x2)-2014,
∴令x1=x2=0,得f(0)=2014,
再令x1+x2=0,将f(0)=2014代入可得f(x)+f(-x)=4028.
设x1<x2,x1,x2∈[-2015,2015],
则x2-x1>0,f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x2-x1)+f(x1)-2014-f(x1)=f(x2-x1-2014>0,
即函数f(x)是递增的,
∴f(x)max=f(2015),f(x)min=f(-2015).
又∵f(2015)+f(-2015)=4028,
∴M+N的值为4028.
故选:D.
点评 本题主要考查函数值的计算,利用赋值法,证明函数的单调性是解决本题的关键,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:选择题
| A. | [-6,6] | B. | [-3,3]∪[5,+∞) | C. | $[{-6,4+\sqrt{6}}]$ | D. | $[{-6,6}]∪[{4+\sqrt{6},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {1,2} | C. | {0,3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
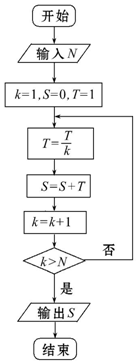
| A. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{10}$ | B. | 1+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+…+$\frac{1}{1×2×…×10}$ | ||
| C. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{11}$ | D. | 1+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+…+$\frac{1}{1×2×…×11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $±\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {0,1} | C. | {0,1,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果两条直线l1与l2垂直,那么它们的斜率之积一定等于-1 | |
| B. | “a>0,b>0”是“$\frac{b}{a}$+$\frac{a}{b}$≥2”的充分必要条件 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “a≠-5或b≠5”是“a+b≠0”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com