
| A. | [-2,1] | B. | [-2,0] | C. | [-1,1] | D. | [-1,0] |
分析 因为偶函数在对称区间上单调性相反,根据已知中f(x)是偶函数,且f(x)在(0,+∞)上是增函数,易得f(x)在(-∞,0)上为减函数,又由若$x∈[{\frac{1}{2}\;,\;1}]$时,不等式f(ax+1)≤f(x-2)恒成立,结合函数恒成立的条件,求出$x∈[{\frac{1}{2}\;,\;1}]$时f(x-2)的最小值,从而可以构造一个关于a的不等式,解不等式即可得到实数a的取值范围.
解答 解:∵f(x)是偶函数,且f(x)在(0,+∞)上是增函数,
∴f(x)在(-∞,0)上为减函数,
当$x∈[{\frac{1}{2}\;,\;1}]$时,x-2∈[-$\frac{3}{2}$,-1],
故f(x-2)≥f(-1)=f(1),
若$x∈[{\frac{1}{2}\;,\;1}]$时,不等式f(ax+1)≤f(x-2)恒成立,
则当$x∈[{\frac{1}{2}\;,\;1}]$时,|ax+1|≤1恒成立,
∴-1≤ax+1≤1,∴$\frac{-2}{x}$≤a≤0,
∴-2≤a≤0,
故选B.
点评 本题的考点是函数恒成立问题,主要考查的知识点是奇偶性与单调性的综合,其中根据已知条件结合偶函数在对称区间上单调性相反,证得f(x)在(-∞,0)上为减函数,进而给出$x∈[{\frac{1}{2}\;,\;1}]$时f(x-2)的最小值,是解答本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 3×223 | B. | 3×224 | C. | 223 | D. | 224 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 总计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 132 | B. | 66 | C. | -132 | D. | -66 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
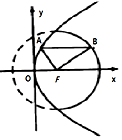 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )| A. | (6,10) | B. | (8,12) | C. | [6,8] | D. | [8,12] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -19 | B. | -7 | C. | -5 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤2} | B. | {1,2} | C. | {x|0<x≤2} | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com