
| 喜欢 | 不喜欢 | 总计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)计算K2的值,与临界值比较,即可得到结论;
(2)确定样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,利用列举法确定基本事件,即可求得结论.
解答 解:(1)${K^2}=\frac{{55{{(20×20-10×5)}^2}}}{30×25×25×30}$≈11.978>7.879,
所以在犯错误的概率不超过0.5%的前提下认为喜欢“人文景观”景点与年龄有关 (5分)
(2)设所抽样本中有m个“大于40岁”市民,则$\frac{m}{20}$=$\frac{6}{30}$,得m=4,所以样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,分别记作B1,B2,B3,B4,C1,C2.
从中任选2人的基本事件有(B1,B2),(B1,B3),(B1,B4),(B1,C1),(B1,C2),(B2,B3),(B2,B4),(B2,C1),(B2,C2),(B3,B4),(B3,C1),(B3,C2),(B4,C1),(B4,C2),(C1,C2),共15个.(10分)
其中恰有1名“大于40岁”和1名“20岁至40岁”的市民的事件有(B1,C1),(B1,C2),(B2,C1),(B2,C2),(B3,C1),(B3,C2),(B4,C1),(B4,C2),共8个.
所以恰有1名“大于40岁”的市民和1名“20岁至40岁”的市民的概率为P=$\frac{8}{15}$.(12分)
点评 本题考查独立性检验,考查概率知识的运用,考查学生的计算能力,利用列举法确定基本事件是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
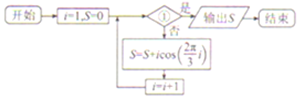
| A. | i>4? | B. | i≥4? | C. | i>3? | D. | i≥3? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x≤2} | C. | {x|2<x≤3} | D. | {x|2≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | [-2,0] | C. | [-1,1] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与ω有关,且与ϕ有关 | B. | 与ω有关,但与ϕ无关 | ||
| C. | 与ω无关,且与ϕ无关 | D. | 与ω无关,但与ϕ有关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com