
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 由条件利用三角函数的恒等变换求得an2α的值,再利用两角和的正切公式求得tan(2α+$\frac{π}{4}$)的值.
解答 解:若$\frac{2co{s}^{2}α+cos(\frac{π}{2}+2α)-1}{\sqrt{2}sin(2α+\frac{π}{4})}$=4=$\frac{cos2α-sin2α}{\sqrt{2}•(sin2α•\frac{\sqrt{2}}{2}+cos2α•\frac{\sqrt{2}}{2})}$=$\frac{1-tan2α}{tan2α+1}$,
∴tan2α=-$\frac{3}{5}$,
则tan(2α+$\frac{π}{4}$)=$\frac{tan2α+tan\frac{π}{4}}{1-tan2α•tan\frac{π}{4}}$=$\frac{-\frac{3}{5}+1}{1-(-\frac{3}{5})•1}$=$\frac{1}{4}$,
故选:C.
点评 本题主要考查三角函数的恒等变换,两角和的正切公式的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
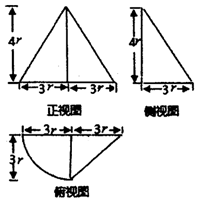 已知一个简单几何的三视图如图所示,若该几何体的体积为24π+48,则该几何体的表面积为( )
已知一个简单几何的三视图如图所示,若该几何体的体积为24π+48,则该几何体的表面积为( )| A. | 24π+48 | B. | $24π+90+6\sqrt{41}$ | C. | 48π+48 | D. | $24π+66+6\sqrt{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M<N | B. | M=N | C. | M>N | D. | M、N大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 总计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 132 | B. | 66 | C. | -132 | D. | -66 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -19 | B. | -7 | C. | -5 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com