
| A. | M<N | B. | M=N | C. | M>N | D. | M、N大小不确定 |
分析 首先,根据锐角三角形的角的特点,A+B>90°C+B>90°A+C>90°,然后,利用诱导公式进行判断,得到sinA>cosB,sinB>cosC,sinC>cosA,最后,利用不等式的性质,从而得到相应的结论.
解答 解:∵△ABC为锐角三角形,
∴A+B>90°,
∴A>90°-B,
∴sinA>sin(90°-B)=cosB,即:sinA>cosB,
同理可得:sinB>cosC,sinC>cosA,
上面三式相加:sinA+sinB+sinC>cosA+cosB+cosC,
∴在锐角△ABC中,sinA+sinB+sinC>cosA+cosB+cosC,
∴M>N,
故选:C.
点评 本题综合考查三角形的性质、诱导公式及其运用等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<0 | B. | 0<a<1 | C. | a>1 | D. | a<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
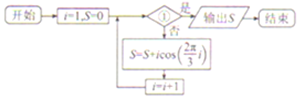
| A. | i>4? | B. | i≥4? | C. | i>3? | D. | i≥3? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
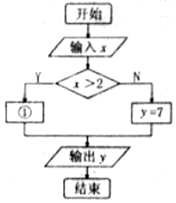 某地区打的士收费办法如下:不超过2公里收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元(其他因素不考虑),计算收费标准的框图如图所示,则①处应填( )
某地区打的士收费办法如下:不超过2公里收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元(其他因素不考虑),计算收费标准的框图如图所示,则①处应填( )| A. | y=2.0x+2.2 | B. | y=0.6x+2.8 | C. | y=2.6x+2.0 | D. | y=2.6x+2.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com