
分析 (Ⅰ)求出函数的导数,根据二次函数的性质证明即可;
(Ⅱ)求出f(α)+f(β)的解析式,根据二次函数的性质以及ACBD均为平行四边形,求出t的值即可.
解答 解:(Ⅰ)证明:$f'(x)=\frac{{4({x^2}+1)-(4x-t)2x}}{{{{({x^2}+1)}^2}}}=\frac{{-4{x^2}+2tx+4}}{{{{({x^2}+1)}^2}}}=0$,
即-4x2+2tx+4=0,△=4t2+64>0,
∴$α+β=\frac{t}{2},α•β=-1$,$f(x)=\frac{4x-t}{{{x^2}+1}}=0$,即4x-t=0,则零点$γ=\frac{t}{4}$,
∴$α+β=2γ=\frac{t}{2}$得证.
(Ⅱ) 要使$A,C({\frac{t}{4}-m,0}),B,D({\frac{t}{4}+m,0})$构成平行四边形,
由$α+β=\frac{t}{2}=({\frac{t}{4}-m})+({\frac{t}{4}+m})$得,只需f(α)+f(β)=0,
∴$f(α)+f(β)=\frac{4α-t}{{{α^2}+1}}+\frac{4β-t}{{{β^2}+1}}=\frac{{4α{β^2}+4α-t{β^2}-t+4{α^2}β+4β-t{α^2}-t}}{{({α^2}+1)({β^2}+1)}}$
=$\frac{{4αβ(α+β)+4(α+β)-t({β^2}+{α^2})-2t}}{{({α^2}+1)({β^2}+1)}}$=$\frac{{-2t+2t-t[{{(β+α)}^2}-2αβ]-2t}}{{({α^2}+1)({β^2}+1)}}$
=$\frac{{-2t-t[\frac{t^2}{4}+2]}}{{({α^2}+1)({β^2}+1)}}=\frac{{-4t-\frac{t^3}{4}}}{{({α^2}+1)({β^2}+1)}}=\frac{{-t(4+\frac{t^2}{4})}}{{({α^2}+1)({β^2}+1)}}=0$,
所以t=0.
点评 本题考查了导数的应用,考查二次函数的性质以及不等式的证明,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
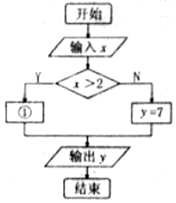 某地区打的士收费办法如下:不超过2公里收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元(其他因素不考虑),计算收费标准的框图如图所示,则①处应填( )
某地区打的士收费办法如下:不超过2公里收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元(其他因素不考虑),计算收费标准的框图如图所示,则①处应填( )| A. | y=2.0x+2.2 | B. | y=0.6x+2.8 | C. | y=2.6x+2.0 | D. | y=2.6x+2.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与ω有关,且与ϕ有关 | B. | 与ω有关,但与ϕ无关 | ||
| C. | 与ω无关,且与ϕ无关 | D. | 与ω无关,但与ϕ有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com