
| A. | $\frac{1}{3}$ | B. | -$\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 对式子|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|两边平方求出$\overrightarrow{a}•\overrightarrow{b}$,从而可得|$\overrightarrow{a}+\overrightarrow{b}$|和$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$,代入投影公式计算即可.
解答 解:∵|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|,∴($\overrightarrow{a}+\overrightarrow{b}$)2=2($\overrightarrow{a}-\overrightarrow{b}$)2,
即2+2$\overrightarrow{a}•\overrightarrow{b}$=4-4$\overrightarrow{a}•\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{3}$.
∴|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2+\frac{2}{3}}$=$\frac{2\sqrt{6}}{3}$,$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=${\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}$=$\frac{4}{3}$,
∴$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$的投影为$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{\frac{4}{3}}{\frac{2\sqrt{6}}{3}}$=$\frac{\sqrt{6}}{3}$.
故选D.
点评 本题考查了平面向量的数量积运算,模长计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x (g) | 5 | 10 | 15 | 20 | 25 | 30 |
| y (cm) | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
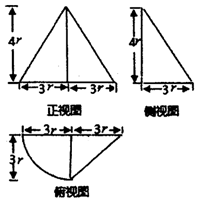 已知一个简单几何的三视图如图所示,若该几何体的体积为24π+48,则该几何体的表面积为( )
已知一个简单几何的三视图如图所示,若该几何体的体积为24π+48,则该几何体的表面积为( )| A. | 24π+48 | B. | $24π+90+6\sqrt{41}$ | C. | 48π+48 | D. | $24π+66+6\sqrt{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3×223 | B. | 3×224 | C. | 223 | D. | 224 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 总计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com