
分析 (1)设d=Asin(ωt+φ)+h,利用低潮时入口处水的深度为8.4m,高潮时为16m,求出h,A,利用两次高潮发生的时间间隔12h,求出ω,再求出φ,即可描述这个港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00,t=17,即可求出水的深度;
(3)d=3.8sin($\frac{π}{6}$t-$\frac{π}{6}$)+12.2≤10.3,即可求出10月10日这一天该港口共有多少时间水深低于10.3m.
解答 解:(1)由题意,$\left\{\begin{array}{l}{A+h=16}\\{-A+h=8.4}\end{array}\right.$,∴h=12.2,A=3.8,
∵T=12,
∴ω=$\frac{π}{6}$,
t=4时,4ω+φ=$\frac{π}{2}$,∴φ=-$\frac{π}{6}$,
∴d=3.8sin($\frac{π}{6}$t-$\frac{π}{6}$)+12.2;
(2)t=17时,d=3.8sin($\frac{π}{6}$×17-$\frac{π}{6}$)+12.2≈15.5;
(3)d=3.8sin($\frac{π}{6}$t-$\frac{π}{6}$)+12.2<10.3,
∴$\frac{7}{6}$π<$\frac{π}{6}$t-$\frac{π}{6}$<$\frac{11}{6}$π,
∴8<t<12,
∴10月10日这一天该港口共有10h水深低于10.3m.
点评 本题考查在实际问题中建立三角函数模型,考查学生利用数学知识解决实际问题,属于中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
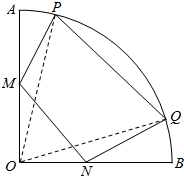 如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.
如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)>0 | D. | f(x1)>0,f(x2)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com