
分析 由条件利用正弦函数的图象的特征,正弦函数的奇偶性、最值、周期性,求得函数f(x)的最小正周期.
解答 解:函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象关于坐标原点中心对称,可得φ=0,
∵f(x)在y轴右侧的第一个极值点为x=$\frac{π}{3}$,∴ω•$\frac{π}{3}$=$\frac{π}{2}$,∴ω=$\frac{3}{2}$,∴函数f(x)=Asin($\frac{3}{2}$x),
则函数f(x)的最小正周期为$\frac{2π}{\frac{3}{2}}$=$\frac{4π}{3}$,
故答案为:$\frac{4}{3}π$.
点评 本题主要考查正弦函数的图象的特征,正弦函数的奇偶性、最值、周期性,属于基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$] | D. | [$\frac{3π}{4}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
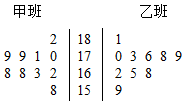 从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.
从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{13π}{48},0)$ | B. | $(\frac{π}{8},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{7π}{12},0)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com