
分析 (1)列举出所有的基本事件和两位专家选择同一个城市的基本事件,使用对立事件的概率关系计算概率;
(2)列举出符合条件的基本事件,使用古典概型的概率公式计算概率.
解答 解:(1)两位专家各随机选取一个城市共有${C}_{3}^{1}$•${C}_{3}^{1}$=9个基本事件,两位专家选择同一个城市的基本事件共有${C}_{3}^{1}$=3个,
∴两位环保专家选取的城市各不相同的基本事件共有6个,
∴两位环保专家选取的城市各不相同的概率为P=$\frac{6}{9}=\frac{2}{3}$.
(2)两位专家至少有一个选择城市A的基本事件有2${C}_{1}^{1}$${C}_{2}^{1}$+${C}_{1}^{1}$${C}_{1}^{1}$=5个,
∴两位环保专家中至少有一名专家选择A城市的概率为P=$\frac{5}{9}$.
点评 本题考查了古典概型的概率计算,属于基础题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{9}{19}$ | D. | $\frac{18}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
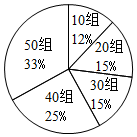 “我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
“我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:| 投票 年龄 | 是 | 否 | 合计 |
| 10组 | |||
| 50组 | |||
| 合计 |
| P(x2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (-∞,-2) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [2,+∞) | C. | [3,+∞) | D. | [4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com