
分析 (Ⅰ)利用an+1=2an+n-1化简$\frac{{a}_{n+1}+(n+1)}{{a}_{n}+n}$即得结论;
(Ⅱ)通过a1=1可知数列{an+n}是首项、公比均为2的等比数列,进而可求出数列{an}的通项公式,进而利用分组法求和计算即得结论.
解答 (Ⅰ)证明:∵an+1=2an+n-1,
∴$\frac{{a}_{n+1}+(n+1)}{{a}_{n}+n}$=$\frac{2{a}_{n}+n-1+(n+1)}{{a}_{n}+n}$=2,
∴数列{an+n}为等比数列;
(Ⅱ)解:∵a1+1=2,
∴数列{an+n}是首项、公比均为2的等比数列,
∴an+n=2n,即an=-n+2n,
∴Sn=-(1+2+…+n)+(21+22+…+2n)
=-$\frac{n(n+1)}{2}$+$\frac{2(1-{2}^{n})}{1-2}$
=2n+1-$\frac{n(n+1)}{2}$-2.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
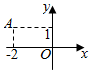 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com