
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,结合数形结合进行求解即可.
解答 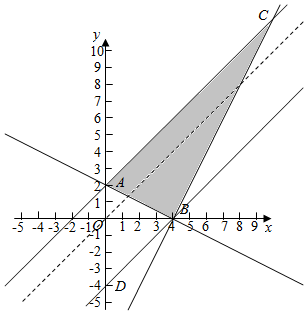 解:由z=y-x得y=x+z,
解:由z=y-x得y=x+z,
作出不等式组对应的平面区域如图(阴影部分ABC):
平移直线y=x+z由图象可知当直线y=x+z经过点B时,直线y=x+z的截距最小,此时z也最小,
由$\left\{\begin{array}{l}{x+2y-4=0}\\{2x-y-8=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$,即B(4,0).
代入目标函数z=y-x,
得z=0-4=-4.
z=$\frac{x}{y+4}$=$\frac{1}{\frac{y+4}{x}}$,
设k=$\frac{y+4}{x}$,则k的几何意义是区域内的点到D(0,-4)的斜率,
由图象知BD的斜率最小,此时k=$\frac{0+4}{4}=1$,
即k≥1,则z=$\frac{1}{k}$∈(0,1],
即z=$\frac{x}{y+4}$的最大值是1,
故答案为:-4;1.
点评 本题主要考查线性规划的应用,利用直线平移以及转化为直线斜率,利用数形结合是解决线性规划问题中的基本方法.综合性较强.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
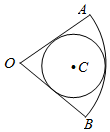 如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )| A. | 450 | B. | 400 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
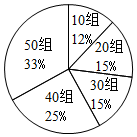 “我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
“我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:| 投票 年龄 | 是 | 否 | 合计 |
| 10组 | |||
| 50组 | |||
| 合计 |
| P(x2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1-\sqrt{2},\sqrt{2}]$ | B. | $[1-\sqrt{2},\sqrt{2}]$ | C. | $[\frac{1}{2},\sqrt{2}]$ | D. | $(\frac{1}{2},\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com