
分析 (1)设C(a,b),a<0,b>0,根据向量的坐标运算和向量的模,以及向量的垂直的条件求出点C的坐标,再根据向量的加减运算求出P的坐标,问题得以解决,
(2)根据向量的坐标运算,以及线性规划,即可求出答案.
解答 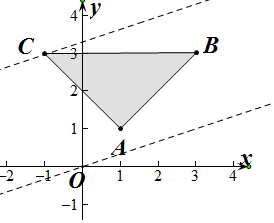 解:(1)设C(a,b),a<0,b>0,
解:(1)设C(a,b),a<0,b>0,
∵A(1,1),B(3,3),
∴$\overrightarrow{AB}$=(2,2),$\overrightarrow{AC}$=(a-1,b-1),
∵△ABC是以∠BAC为直角的等腰直角三角形,
∴|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|,$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,
∴$\left\{\begin{array}{l}{(a-1)^{2}+(b-1)^{2}={2}^{2}+{2}^{2}}\\{2(a-1)+2(b-1)=0}\end{array}\right.$,
解得a=-1,b=3
∴C(-1,3),
设P(x,y),
∵$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,
∴(1-x,1-y)+(3-x,3-y)+(-1-x,3-y)=(0,0),
∴3-3x=0,7-3y=0
∴x=1,y=$\frac{7}{3}$,
∴P(1,$\frac{7}{3}$),
∴|${\overrightarrow{OP}}$|=$\sqrt{{1}^{2}+(\frac{7}{3})^{2}}$=$\frac{\sqrt{58}}{3}$
(2)∵$\overrightarrow{AC}$=(-2,2),$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$(m,n∈R),
∴(x,y)=m(2,2)+n(-2,2)=(2m-2n,2m+2n),
∴x=2m-2n,y=2m+2n,
∴m=$\frac{1}{4}$(x+y),2n=$\frac{1}{2}$(y-x),
∴m+2n=-$\frac{1}{4}$x+$\frac{3}{4}$y,
设z=3y-x,直线z=3y-x经过点C(-1,3)时,z取得最大值,
即m+2n=$\frac{1}{4}$+$\frac{3}{4}$×3=$\frac{5}{2}$.
点评 本题考查了平面向量的数乘及坐标加法运算,考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | f($\frac{3}{4}$)<f(a2-a+1) | B. | f($\frac{3}{4}$)>f(a2-a+1) | C. | f($\frac{3}{4}$)≤f(a2-a+1) | D. | f($\frac{3}{4}$)≥f(a2-a+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或1 | B. | 0 | C. | 0或2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
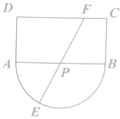 如城某观光区的平面示意图如图所示,其中矩形ABCD的长AB=2千米,宽AD=1千米,半圆的圆心P为AB中点,为了便于游客观光休闲,在观光区铺设一条由圆弧$\widehat{AE}$、线段EF、FC组成的观光道路,其中线段EF经过圆心P,且点F在线段CD上(不含线段端点C,D),已知道路AE,FC的造价为2a(a>0)元每千米,道路EF造价为7a元每千米,设∠APE=θ,观光道路的总造价为y.
如城某观光区的平面示意图如图所示,其中矩形ABCD的长AB=2千米,宽AD=1千米,半圆的圆心P为AB中点,为了便于游客观光休闲,在观光区铺设一条由圆弧$\widehat{AE}$、线段EF、FC组成的观光道路,其中线段EF经过圆心P,且点F在线段CD上(不含线段端点C,D),已知道路AE,FC的造价为2a(a>0)元每千米,道路EF造价为7a元每千米,设∠APE=θ,观光道路的总造价为y.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0) | B. | [-1,0)∪(0,+∞) | C. | (0,+∞) | D. | [-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com