
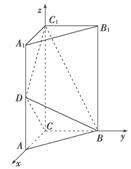
如图,直三棱柱ABC-A1B1C1中,AC=BC=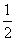 AA1,D是棱AA1的中点,DC1⊥BD.
AA1,D是棱AA1的中点,DC1⊥BD.
(1)证明:DC1⊥BC;
(2)求二面角A1-BD-C1的大小.
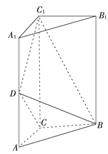
解 :(1)证明:由题设知,三棱柱的侧面为矩形.由于D为AA1的中点,故DC=DC1.又AC=
:(1)证明:由题设知,三棱柱的侧面为矩形.由于D为AA1的中点,故DC=DC1.又AC=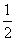 AA1,可得DC
AA1,可得DC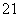 +DC2=CC
+DC2=CC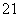 ,
,
所以DC1⊥DC.
而DC1⊥BD,DC∩BD=D,
所以DC1⊥平面BCD.
又BC⊂平面BCD,
故DC1⊥BC.
(2)由(1)知BC⊥DC1,且BC⊥CC1,则BC⊥平面ACC1A1,所以CA,CB,CC1两两相互垂直.
以C为坐标原点,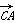 的方向为x轴的正方向,|
的方向为x轴的正方向,|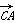 |为单位长,建立如图所示的空间直角坐标系Cxyz.
|为单位长,建立如图所示的空间直角坐标系Cxyz.
由题意知A1(1,0,2),B(0,1,0),D(1,0,1),C1(0,0,2).
则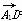 =(0,0,-1),
=(0,0,-1),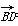 =(1,-1,1),
=(1,-1,1),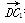 =(-1,0,1).
=(-1,0,1).
设n=(x,y,z)是平面A1B1BD的法向量,则
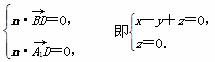 可取n=(1
可取n=(1 ,1,0).
,1,0).
同理,设m是平面C1BD的法向量,则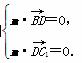 可取m=(1,2,1).
可取m=(1,2,1).
从而cos〈n,m〉=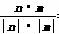 =
=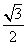 .
.
故二面角A1-BD-C1的大小为30°.


科目:高中数学 来源: 题型:

如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB>1,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2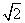 .
.
(1)求AB的长度;
(2)求该长方体外接球的表面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l、m,平面α、β,且l⊥α,m⊂β,则α∥β是l⊥m的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD垂足为H,PH是四棱锥的高,E为AD的中点.
(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.
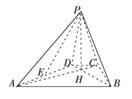
查看答案和解析>>
科目:高中数学 来源: 题型:
一支田径队有男女运动员98人,其中男运动员有56人,按男女比例用分层抽样的方 法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是________.
法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,11 0),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
0),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
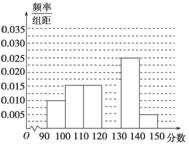
(1)求分数在[120,130)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l的倾斜角为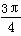 ,直线l1经过点A(3,2)、B(a,-1),且l1与l垂直,直线l2:2x
,直线l1经过点A(3,2)、B(a,-1),且l1与l垂直,直线l2:2x +by+1=0与直线l1平行,则a+
+by+1=0与直线l1平行,则a+ b等于( )
b等于( )
A.-4 B.-2
C.0 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com