练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

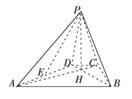
    如图，已知四棱锥P－ABCD的底面为等腰梯形，AB∥CD，AC⊥BD垂足为H，PH是四棱锥的高，E为AD的中点．

    (1)证明：PE⊥BC；

    (2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值．


    解：

    以H为原点，HA、HB、HP所在直线分别为x轴，y轴，z轴，线段HA的长为单位长，建立空间直角坐标系如图，

    则A(1,0,0)，B(0,1,0).

    (1)证明：设C(m,0,0)，P(0,0，n)(m＜0，n＞0)．

    则D(0，m,0)，E

    可得＝．

    因为·＝－＋0＝0，

    所以PE⊥BC.

    (2)由已知条件及(1)可得m＝－，n＝1，则P(0,0,1)．

    ＝，＝(－1,0,1)．

    由(1)知为面PEH的一个法向量．

    因此直线PA与平面PEH所成角的正弦值为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设P表示一个点，a，b表示两条直线，α，β表示两个平面，给出下列四个命题，其中正确的命题是(　　)

    ①P∈a，P∈α⇒a⊂α；

    ②a∩b＝P，b⊂β⇒a⊂β；

    ③a∥b，a⊂α，P∈b，P∈α⇒b⊂α；

    ④α∩β＝b，P∈α，P∈β⇒P∈b.

    A．①②                           B．②③

    C．①④                           D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若向量a＝(1，λ，2)，b＝(－2,1,1)，a，b夹角的余弦值为，则λ等于(　　)

    A．1　　　　　　　　           B．－1

    C．±1                         D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


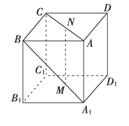
    如图所示，在正方体ABCD－A1B1C1D1中，棱长为a，M，N分别为A1B和AC上的点，A1M＝AN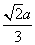＝，则MN与平面BB1C1C的位置关系是(　　)

    A．相交                            B．平行

    C．垂直                            D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


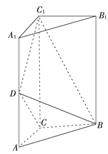
    如图，直三棱柱ABC－A1B1C1中，AC＝BC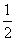＝AA1，D是棱AA1的中点，DC1⊥BD.

    (1)证明：DC1⊥BC；

    (2)求二面角A1－BD－C1的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列说法中正确的个数是(　　)

    ①总体中的个体数不多时宜用简单随机抽样法；

    ②在总体均分后的每一部分进行抽样时，采用的是简单随机抽样；

    ③百货商场的抓奖活动是抽签法；

    ④整个抽样过程中，每个个体被抽取的概率相等(有剔除时例外)．

    A．1                              B．2

    C．3                              D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名．现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为(　　)

    A．6                              B．8

    C．10                             D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    把容量为100的某个样本数据分为10组，并填写频率分布表，若前七组的累积频率为0.79，而剩下三组的频数成公比为大于2的整数的等比数列，则剩下三组中频数最高的一组的频数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两直线l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0.求分别满足下列条件的a，b的值．

    (1)直线l1过点(－3，－1)，并且直线l1与l2垂直；

    (2)直线l1与直线l2平行，并且坐标原点到l1，l2的距离相等．

    查看答案和解析>>

    同步练习册答案