
分析 (1)设出椭圆的标准方程,利用实轴长为12,离心率为$\frac{2}{3}$,即可求得几何量,从而可得椭圆的标准方程;
(2)根据圆心坐标与半径,可直接写出圆的标准方程;
(3)设抛物线方程为y2=2px(p>0),根据题意建立关于p的方程,解之可得p=$\frac{1}{2}$,得到抛物线方程;
(4)设双曲线方程为mx2-ny2=1(m>0,n>0),代入点$(-\sqrt{2}$,-$\sqrt{3}$),($\frac{{\sqrt{15}}}{3}$,$\sqrt{2}$),可得方程组,求出m,n,即可求双曲线的标准方程.
解答 解:(1)设椭圆的标准方程为 $\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)
∵实轴长为12,离心率为$\frac{2}{3}$,
∴a=6,$\frac{c}{a}$=$\frac{2}{3}$,
∴c=4,∴b2=a2-c2=20
∴椭圆的标准方程为$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1;
(2)依题意得,该圆的半径为:$\sqrt{(5-8)^{2}+(1+3)^{2}}$=5.
所以圆的标准方程是(x-8)2+(y+3)2=25;
(3)由题意,设抛物线的标准方程为y2=2px(p>0),
∵抛物线的准线方程为x=-$\frac{1}{4}$,
∴$\frac{p}{2}$=$\frac{1}{4}$,解得p=$\frac{1}{2}$,
故所求抛物线的标准方程为y2=x.
(4)设双曲线方程为mx2-ny2=1(m>0,n>0),
代入点$(-\sqrt{2}$,-$\sqrt{3}$),($\frac{{\sqrt{15}}}{3}$,$\sqrt{2}$),可得$\left\{\begin{array}{l}{2m-3n=1}\\{\frac{5m}{3}-2n=1}\end{array}\right.$,
∴m=1,n=$\frac{1}{3}$,
∴双曲线的标准方程为x2-$\frac{1}{3}$y2=1.
点评 本题给出抛物线的准线,求抛物线的标准方程,着重考查了抛物线的定义与标准方程的知识,考查双曲线方程,圆的标准方程,属于基础题.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| P(k2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 0.1% | B. | 1% | C. | 99% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
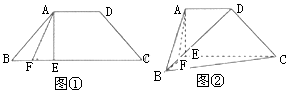 如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.
如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x1)≤f(x)≤f(x2)对?x∈R恒成立,则|x2-x1|min=π | |
| B. | y=f(x)的图象关于点(-$\frac{2π}{3}$,0)中心对称 | |
| C. | 函数f(x)的单调区间为:[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | |
| D. | 函数y=|f(x)|(x∈R)的图象相邻两条对称轴之间的距离是$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-5 | B. | y=$\frac{{x}^{2}+1}{x}$ | C. | y=2x+log2x | D. | y=3x+3-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com