
���� �����ݺ��������ʣ�����ֱ�����жϼ��ɣ�
��� �⣺��1����x1=1��x2=2ʱ��f��x1+x2��=f��2��=$\sqrt{2}$��f��x1��•f��x2��=1��1=1�������
��2��f��x1•x2��=$\sqrt{{x}_{1}{x}_{2}}$=$\sqrt{{x}_{1}}$•$\sqrt{{x}_{2}}$=f��x1��•f��x2��������ȷ��
��3��$\frac{{f��{x_1}��-f��{x_2}��}}{{{x_1}-{x_2}}}$��0���ຯ��f��x��=${x}^{\frac{1}{2}}$Ϊ������������ȷ��
��4��f��$\frac{{{x_1}+{x_2}}}{2}$����$\frac{{f��{x_1}��+f��{x_2}��}}{2}$�ĺ���Ϊ����������ȷ��
�ʣ�2����3����4����ȷ��
�ʴ�Ϊ��2����3����4��
���� ������Ҫ�����ݺ�����ͼ������ʣ�Ҫ����������ָ���ݵ����㣬���ݺ��������ʣ�


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
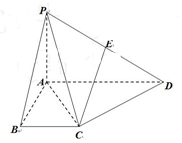 ����ͼ��ʾ������P-ABCD�У���֪PA��ƽ��ABCD��AD��BC����BAD=90�㣬PA=AB=BC=1��AD=2��EΪPD���е㣮
����ͼ��ʾ������P-ABCD�У���֪PA��ƽ��ABCD��AD��BC����BAD=90�㣬PA=AB=BC=1��AD=2��EΪPD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{16��}$ | B�� | $\frac{{\sqrt{2}}}{8��}$ | C�� | $\frac{{\sqrt{2}}}{4��}$ | D�� | $\frac{{\sqrt{2}}}{2��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��0 | B�� | k��1 | C�� | 0��k��1 | D�� | k��1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com