练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．2016年2月份海城市工商局对35种商品进行抽样检查，鉴定结果有15种假货，现从35种商品中选取3种．
    （1）恰有2种假货在内的不同取法有多少种？
    （2）至少有2种假货在内的不同取法有多少种？

    分析 （1）分析可得，从15种假货中取2件，再从20件正品商品中，再取1件即可，由乘法原理计算可得答案；
    （2）根据题意，分有2种假货在内与有3种假货在内，两种情况讨论，分别求得其情况数目，由加法原理计算可得答案．

    解答 解：（1）根据题意，从15种假货中取2件，再从20件正品商品中，再取1件即可，
    由乘法原理，可得有C152•C201=2100种不同方法；
    （2）根据题意，有2种假货在内，不同的取法有C152•C201种，
    有3种假货在内，不同的取法有C153种，
    由加法原理，可得共有C152•C201+C153=2555．

    点评 本题考查排列、组合的综合应用，注意结合分类、分步计数原理，进行综合分析．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．从3双不同的鞋中任取2只，则取出的2只鞋不能成双的概率为（　　）
    A．$\frac{3}{5}$B．$\frac{8}{15}$C．$\frac{4}{5}$D．$\frac{7}{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．甲、乙两人进行射击比赛，他们击中目标的概率分别为$\frac{3}{4}$和$\frac{2}{3}$（两人是否击中目标相互独立），若两人各射击2次，则两人击中目标的次数相等的概率为（　　）
    A．$\frac{1}{6}$B．$\frac{25}{144}$C．$\frac{5}{12}$D．$\frac{61}{144}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设i是虚数单位，a∈R，若i（ai+2）是一个纯虚数，则实数a的值为（　　）
    A．-$\frac{1}{2}$B．-1C．0D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某校对高三部分学生的数学质检成绩作相对分析．

    （1）按一定比例进行分层抽样抽取了20名学生的数学成绩，并用茎叶图（图1）记录，但部分数据不小心丢失了，已知数学成绩[70，90）的频率是0.2，请补全表格并绘制相应频率分布直方图（图2）．
     分数段（分）[50，70）[70，90）[90，110）[110，130）[130，150）
     $\frac{频率}{组距}$ 
    0.005    		 
    0.010    		 
    0.020    		 
    0.010    		 
    0.005
    （2）为考察学生的物理成绩与数学成绩是否有关系，抽取了部分同学的数学成绩与物理成绩进行比较，得到统计数据如表：
      物理成绩优秀 物理成绩一般合计 
     数学成绩优秀 15 3 18
     数学成绩一般 5 17 22
     合计 2020 40 
    能够有多大的把握，认为物理成绩优秀与数学成绩优秀有关系？
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
     P（K2≥K0） 0.05 0.01 0.005 0.001
     K0 3.481 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知f（x）=x+ln$\frac{x}{100-x}$，则f（1）+f（2）+f（3）+…+f（99）的值为（　　）
    A．5000B．4950C．99D．$\frac{99}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．某班生活委员为了解在春天本班同学感冒与性别是否相关，他收集了3月份本班同学的感冒数据，并制出下面一个2×2列联表：
    感冒不感冒合计
    男生52732
    女生91928
    合计134760
    参考数据
    P（K2≥2.072）≈0.15
    P（K2≥2.706）≈0.10
    P（K2≥6.635）≈0.010
    由K2的观测值公式，可求得k=2.278，根据给出表格信息和参考数据，下面判断正确的是（　　）
    A．在犯错概率不超过10%的前提下认为该班“感冒与性别有关”
    B．在犯错概率不超过10%的前提下不能认为该班“感冒与性别有关”
    C．有15%的把握认为该班“感冒与性别有关”
    D．在犯错概率不超过10%的前提下认为该班“感冒与性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若随机变量X的分布列为P（X=i）=$\frac{i}{10}$（i=1，2，3，4），则P（X＞2）=0.7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

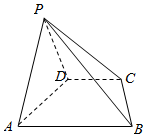    19．如图，四棱锥中P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°．
    （Ⅰ）求证：AD⊥PB；
    （Ⅱ）求平面PAD与平面PBC所成锐二面角的余弦值．

    查看答案和解析>>

    同步练习册答案