Question

4．记max{a，b}=$\left\{\begin{array}{l}{a，a≥b}\\{b，a＜b}\end{array}\right.$，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$•$\overrightarrow{b}$=0，$\overrightarrow{c}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$（λ，μ≥0，且λ+μ=1，则当max{$\overrightarrow{c}$•$\overrightarrow{a}$，$\overrightarrow{c}$•$\overrightarrow{b}$}取最小值时，|$\overrightarrow{c}$|=（　　）

• A． $\frac{2\sqrt{5}}{5}$
• B． $\frac{2\sqrt{2}}{3}$
• C． 1
• D． $\frac{\sqrt{5}}{2}$

Answer 1

分析 由题意画出图形，设$\overrightarrow{OA}=\overrightarrow{a}，\overrightarrow{OB}=\overrightarrow{b}$，则$\overrightarrow{a}=（1，0），\overrightarrow{b}=（0，2）$，由已知求得λ的范围，把$\overrightarrow{c}$•$\overrightarrow{a}$，$\overrightarrow{c}$•$\overrightarrow{b}$均用含有λ的代数式表示，求出分段函数的值域，得到max{$\overrightarrow{c}$•$\overrightarrow{a}$，$\overrightarrow{c}$•$\overrightarrow{b}$}的最小值，进一步求得|$\overrightarrow{c}$|．

解答 解：如图，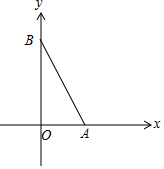

设$\overrightarrow{OA}=\overrightarrow{a}，\overrightarrow{OB}=\overrightarrow{b}$，则$\overrightarrow{a}=（1，0），\overrightarrow{b}=（0，2）$，
∵λ，μ≥0，λ+μ=1，∴0≤λ≤1．
又$\overrightarrow{c}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$，
∴$\overrightarrow{c}•\overrightarrow{a}=（λ\overrightarrow{a}+\overrightarrow{b}-λ\overrightarrow{b}）•\overrightarrow{a}$=λ；
$\overrightarrow{c}•\overrightarrow{b}=（λ\overrightarrow{a}+\overrightarrow{b}-λ\overrightarrow{b}）•\overrightarrow{b}$=4-4λ．
由λ=4-4λ，得$λ=\frac{4}{5}$．
∴max{$\overrightarrow{c}$•$\overrightarrow{a}$，$\overrightarrow{c}$•$\overrightarrow{b}$}=$\left\{\begin{array}{l}{λ，\frac{4}{5}≤λ≤1}\\{4-4λ，0≤λ＜\frac{4}{5}}\end{array}\right.$．
令f（λ）=$\left\{\begin{array}{l}{λ，\frac{4}{5}≤λ≤1}\\{4-4λ，0≤λ＜\frac{4}{5}}\end{array}\right.$．
则f（λ）∈[$\frac{4}{5}，1$]．
∴$f（λ）_{min}=\frac{4}{5}$，此时$λ=\frac{4}{5}，μ=\frac{1}{5}$，
∴$\overrightarrow{c}=\frac{4}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$=$（\frac{4}{5}，\frac{2}{5}）$．
∴$|\overrightarrow{c}|=\sqrt{（\frac{4}{5}）^{2}+（\frac{2}{5}）^{2}}=\frac{2\sqrt{5}}{5}$．
故选：A．

点评 本题考查平面向量的数量积运算，考查数学转化思想方法，训练了分段函数值域的求法，属中档题．