
分析 ①,标准方程的等轴双曲线的渐近线是y=±x;
②,在△ABC中,“若sinA=sinB⇒2RsinA=2RsinB⇒a=b⇒A=B;
③,若动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为线段F1F2;
④,当数列为an=an-1=an+1=0时,“{an}不为等比数列;
⑤,由c=2bcosA,利用正弦定理化简得:sinC=2sinBcosA,得:sinAcosB+cosAsinB=2sinBcosA,即sinAcosB-cosAsinB=sin(A-B)=0,即A=B
解答 解:对于①,标准方程的等轴双曲线的渐近线是y=±x,故错;
对于②,在△ABC中,“若sinA=sinB⇒2RsinA=2RsinB⇒a=b⇒A=B,故正确;
对于③,若动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为线段F1F2,故错;
对于④,当数列为an=an-1=an+1=0时,尽管满足“an2=an-1•an+1”,但“{an}不为等比数列,故错;
对于⑤,由c=2bcosA,利用正弦定理化简得:sinC=2sinBcosA,把sinC=sin(A+B)=sinAcosB+cosAsinB代入得:sinAcosB+cosAsinB=2sinBcosA,
即sinAcosB-cosAsinB=sin(A-B)=0,即A-B=0,∴A=B,即a=b,则△ABC为等腰三角形,故正确;
故答案为:②⑤
点评 本题考查了命题真假的判定,属于基础题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{y}^{2}}{3}$-x2=1 | D. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-25,-$\frac{1}{2}$] | B. | [-5,-$\frac{1}{2}$] | C. | [-25,-1] | D. | [-5,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
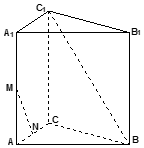 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com