
分析 (1)若恰在第2次测试时,才测到第一件次品,第8次才找到最后一件次品,若是不放回地逐个抽取测试,第2次测到第一件次品有4种方法;第8次测到最后一件次品有3种方法;第3至第7次抽取测到最后两件次品共有${A}_{5}^{2}$种方法;剩余4次抽到的是正品,分类计数原理共有${A}_{4}^{2}$${A}_{5}^{2}$${A}_{6}^{4}$种抽法.
(2)检测4次可测出4件次品,不同的测试方法有${A}_{4}^{4}$种,检测5次可测出4件次品,不同的测试方法有4${A}_{4}^{3}$${A}_{6}^{1}$种;检测6次测出4件次品或6件正品,则不同的测试方法共有4${A}_{5}^{3}$${A}_{6}^{2}$+${A}_{6}^{6}$种,由分类计数原理,知满足条件的不同测试方法的种数为${A}_{4}^{4}$+4${A}_{4}^{3}$${A}_{6}^{1}$+4${A}_{5}^{3}$${A}_{6}^{2}$+${A}_{6}^{6}$.
解答 解:(1)若恰在第2次测试时,才测到第一件次品,第8次才找到最后一件次品,若是不放回地逐个抽取测试,
第2次测到第一件次品有4种方法;第8次测到最后一件次品有3种方法;
第3至第7次抽取测到最后两件次品共有${A}_{5}^{2}$种方法;剩余4次抽到的是正品,共有${A}_{4}^{2}$${A}_{5}^{2}$${A}_{6}^{4}$=86400种抽法.
(2)检测4次可测出4件次品,不同的测试方法有${A}_{4}^{4}$种,
检测5次可测出4件次品,不同的测试方法有4${A}_{4}^{3}$${A}_{6}^{1}$种;
检测6次测出4件次品或6件正品,则不同的测试方法共有4${A}_{5}^{3}$${A}_{6}^{2}$+${A}_{6}^{6}$种.
由分类计数原理,
知满足条件的不同测试方法的种数为${A}_{4}^{4}$+4${A}_{4}^{3}$${A}_{6}^{1}$+4${A}_{5}^{3}$${A}_{6}^{2}$+${A}_{6}^{6}$=8520.
点评 本题考查分步计数问题,考查排列组合的实际应用,考查用排列组合数表示方法数,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\sqrt{5}-1$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
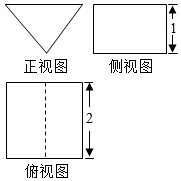 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 2 | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com