
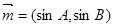 ,
,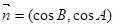 ,
,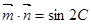 ,且
,且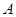 、
、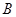 、
、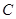 分别为
分别为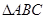 的三边
的三边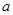 、
、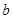 、
、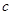 所对的角。
所对的角。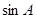 ,
,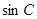 ,
,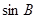 成等差数列,且
成等差数列,且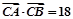 ,求
,求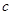 边的长。
边的长。 (2)
(2)
 将cosC的值代入求出ab的值,接着利用余弦定理得到c2=a2+b2-2abcosC,根据完全平方公式变形后,将cosC,a+b,及ab代入得到关于c的方程,求出方程的解即可得到c的值.
将cosC的值代入求出ab的值,接着利用余弦定理得到c2=a2+b2-2abcosC,根据完全平方公式变形后,将cosC,a+b,及ab代入得到关于c的方程,求出方程的解即可得到c的值. …………2分
…………2分 ,
, …………3分
…………3分 ,
, …………6分
…………6分 ,
, …………8分
…………8分 ,
, …………10分
…………10分 , …………11分
, …………11分 ,
, …………12分
…………12分

科目:高中数学 来源:不详 题型:单选题
 (a,b, c分别为角A、B、C的对边),则△ABC的形状为
(a,b, c分别为角A、B、C的对边),则△ABC的形状为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com