Question

7．在某次足球比赛中，对甲、乙两队上场的13名球员（包括10名首发和3名替补登场（守门员除外））的跑动距离（单位：km）进行统计分析，得到的统计结果如茎叶图所示，其中茎表示整数部分，叶表示小数部分．
（1）根据茎叶图求两队球员跑动距离的中位数和平均值（精确到小数点后两位），并给出一个正确的统计结论；
（2）规定跑动距离为9.0km及以上的球员为优秀球员，跑动距离为8.5km及以上的球员为积极球员，其余为一般球员．现从两队的优秀球员中随机抽取2名，求这2名球员中既有甲队球员又有乙队球员的概率

Answer 1

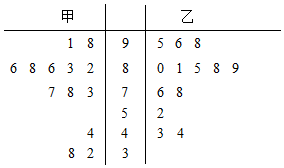
分析 （1）由茎叶图可知甲队球员跑动距离的中位数和乙队球员跑动距离的中位数，求出甲队球员跑动距离的平均数和乙队球员跑动距离的平均数，由于跑动距离的平均值反映的是两队球员跑动的平均距离，球员跑动的积极程度不能通过中位数的对比来下结论．
（2）根据茎叶图可知，两队的优秀球员共5名，其中甲队2名，乙队3名．由此利用列举法能求出这2名球员中既有甲队球员又有乙队球员的概率．

解答 解：（1）由茎叶图可知，甲队球员跑动距离的中位数为8.2km，
乙队球员跑动距离的中位数为8.1km，…（2分）
甲队球员跑动距离的平均数为：
$\frac{9.1+9.8+8.6+8.8+8.6+8.3+8.2+7.7+7.8+7.3+4.4+3.8+3.2}{13}≈7.35km$..（3分）
乙队球员跑动距离的平均数为：
$\frac{9.5+9.6+9.8+8.0+8.1+8.5+8.8+8.9+7.6+7.8+5.2+4.3+4.4}{13}≈7.73km$..（4分）
由于跑动距离的平均值反映的是两队球员跑动的平均距离，
因而可知乙队球员相对甲队球员跑动的更加积极，
而从中位数对比可知甲队球员跑动距离的中位数比乙队球员跑动距离的中位数大，
因而球员跑动的积极程度不能通过中位数的对比来下结论．…（6分）
（2）根据茎叶图可知，两队的优秀球员共5名，其中甲队2名，乙队3名．
将甲队的2名优秀球员分别记为a，b，乙队的3名优秀球员分别记为A，B，C，则从中随机抽取2名，
所有可能的结果为ab，aA，aB，aC，bA，bB，bC，AB，AC，BC共10个．（9分）
其中既有甲队球员又有乙队球员（记为事件M）包含的结果为aA，aB，aC，bA，bB，bC共6个…（11分）
由古典概型的概率计算公式知，这2名球员中既有甲队球员又有乙队球员的概率为：
$P（M）=\frac{6}{10}=\frac{3}{5}$．…（12分）

点评 本题考查茎叶图的应用，考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．