
| A. | 2 | B. | 4 | C. | $\sqrt{5}$+1 | D. | $\sqrt{3}$+1 |
分析 设向量$\overrightarrow a$,$\overrightarrow a$+2$\overrightarrow b$对应点分别为A、B 向量$\overrightarrow c$对应点C,利用向量的几何意义得到坐标运算得到由$|{\overrightarrow c-\overrightarrow a-2\overrightarrow b}|$=1知点C在以B为圆心,半径为1的圆上,由最大距离为d+r即可得到.
解答 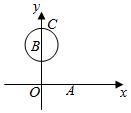 解:设向量$\overrightarrow a$,$\overrightarrow a$+2$\overrightarrow b$对应点分别为A、B 向量$\overrightarrow c$对应点C,
解:设向量$\overrightarrow a$,$\overrightarrow a$+2$\overrightarrow b$对应点分别为A、B 向量$\overrightarrow c$对应点C,
由$|{\overrightarrow c-\overrightarrow a-2\overrightarrow b}|$=1知点C在以B为圆心,半径为1的圆上.
∴$|{\overrightarrow c}|$max=|OB|+1=$|{\overrightarrow a+2\overrightarrow b}|$+1
∵$|{\overrightarrow a+2\overrightarrow b}|$2=$|{\overrightarrow a}|$2+$4|{\overrightarrow b}|$2+4$\overrightarrow a•\overrightarrow b$,
又∵$\overrightarrow a$•($\overrightarrow a$+2$\overrightarrow b$)=0,
∴$|{\overrightarrow a}|$2+2$\overrightarrow a$•$\overrightarrow b$=0
∴2$\overrightarrow a$•$\overrightarrow b$=-1,
∴4$\overrightarrow a$•$\overrightarrow b$=-2,
∴$|{\overrightarrow a+2\overrightarrow b}|$2=1+4-2=3,
∴$|{\overrightarrow a+2\overrightarrow b}|$=$\sqrt{3}$
∴$|{\overrightarrow c}|$max=$\sqrt{3}+1$,
故选:D
点评 本题考查向量的数量积的定义及向量的几何意义,考查运用圆的方程解决最值问题是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图是为求S=1+$\frac{1}{2}$+$\frac{1}{3}$+…$\frac{1}{100}$的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
如图是为求S=1+$\frac{1}{2}$+$\frac{1}{3}$+…$\frac{1}{100}$的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE=CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE=CF=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com