
 �������涨��ѧ��ÿ����������������һ��Сʱ������ѧУ����ִ�У����������������ݱ��Ϊ�˼��ѧУ����������չ�������ѧУ�����ȡ��20���ˣ�������Ŀ�϶��ѧ������ԭ���μ�������ÿ���������ë��ʱ��֮�ͣ������ʱ����Ϊ��ͬѧ�����������ʱ�䣮��֪��20���˵����������ʱ�䶼��3Сʱ��8Сʱ֮�䣬�����Ƴ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�������涨��ѧ��ÿ����������������һ��Сʱ������ѧУ����ִ�У����������������ݱ��Ϊ�˼��ѧУ����������չ�������ѧУ�����ȡ��20���ˣ�������Ŀ�϶��ѧ������ԭ���μ�������ÿ���������ë��ʱ��֮�ͣ������ʱ����Ϊ��ͬѧ�����������ʱ�䣮��֪��20���˵����������ʱ�䶼��3Сʱ��8Сʱ֮�䣬�����Ƴ���ͼ��Ƶ�ʷֲ�ֱ��ͼ������ �� I����ֱ��ͼ�����ʿɵ�x�ķ��̣��ⷽ�̿ɵ�xֵ�������ɵ���[6��8]Сʱ������Ϊ��
��II���ɣ� I���ɵûʱ����[6��7��Сʱ������Ϊ3����[7��8]Сʱ������Ϊ2���ֱ��ʾΪA1��A2��A3��B1��B2���оٿɵ��ܵĻ����¼���10���������������6�����ɸ��ʹ�ʽ�ɵã�
��� �⣺�� I�������Ϊ1������ֱ��ͼ�ɵ�[3��4����[4��5����[5��6����
[6��7����[7��8]��Ƶ�ʷֱ�Ϊ0.1��0.25��0.4��x��0.1��
��0.1+0.25+0.4+x+0.1=1���ⷽ�̿ɵ�x=0.15
�߳�ȡ20���ˣ���һ�������������ʱ����[6��8]Сʱ������Ϊ20����0.15+0.1��=5��
��һ�������������ʱ����[6��8]Сʱ������Ϊ5��
��II���ɣ� I����һ�������������ʱ����[6��7��Сʱ������Ϊ3����[7��8]Сʱ������Ϊ2��
�ֱ��ʾΪA1��A2��A3��B1��B2������5�����г�ȡ2���ˣ������»����¼���
A1A2��A1A3��A1B1��A1B2��A2A3��A2B1��A2B2��A3B1��A3B2��B1B2����10����
����ǡ��һ���˵����������ʱ����[6��7��Сʱ�Ļ����¼���6�������¼���
�衰ǡ��1���˵����������ʱ����[6��7��Сʱ���¼�M����$P��M��=\frac{6}{10}=\frac{3}{5}$
���� ���⿼���оٷ���������¼����Լ��¼������ĸ��ʣ��漰ֱ��ͼ�����ʣ��������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
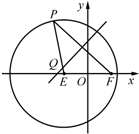 ��ͼ����֪ԲE��${��x+\sqrt{3}��^2}+{y^2}$=16����$F��\sqrt{3}��0��$��P��ԲE������һ�㣮�߶�PF�Ĵ�ֱƽ���ߺͰ뾶PE�ཻ��Q��
��ͼ����֪ԲE��${��x+\sqrt{3}��^2}+{y^2}$=16����$F��\sqrt{3}��0��$��P��ԲE������һ�㣮�߶�PF�Ĵ�ֱƽ���ߺͰ뾶PE�ཻ��Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��֪p��?x0��R��x02+x0-1=0��q��?x��R��x2+x+1��0����p��q�������� | |
| B�� | ����p����$\overrightarrow a��\overrightarrow b$����$\overrightarrow a•\overrightarrow b=0$�ķ������ǣ���$\overrightarrow a��\overrightarrow b$����$\overrightarrow a•\overrightarrow b��0$ | |
| C�� | ?x��R��x2+x-1��0�ķ���?x0��R��x02+x0-1��0 | |
| D�� | x=$\frac{��}{3}$��$y=sin��2x-\frac{��}{6}��$ȡ���ֵ�ij�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����f��x��������Ϊ$\frac{��}{2}$ | |
| B�� | ����f��x����ֵ��ΪR | |
| C�� | �㣨$\frac{��}{6}$��0���Ǻ���f��x����ͼ��һ���Գ����� | |
| D�� | f��$\frac{2��}{5}$����f��$\frac{3��}{5}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m��n?����m�֣�n�֣������ | B�� | ��m?�������֣���m�� | ||
| C�� | ��m�ͦ������ͦ£�n�Φ£���m��n | D�� | �����ͦã��¡ͦã�����ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com