
分析 (Ⅰ)利用函数的导数求出切线的斜率,将x=1代入,求得y=$-\frac{1}{2}$,(Ⅱ)利用导数符号判断函数的单调区间,(Ⅲ),先将h(x)写出,进行化简,求得h(x)在定义域内单调递增,利用零点定理,判断h(x)有一个零点.
解答 解:(Ⅰ)函数f(x)=lnx-$\frac{{x}^{2}}{2}$,(x>0)f′(x)=$\frac{1}{x}$-x,
在x=1处的切线方程的斜率为k=f′(1)=0,
∴求曲线y=f(x)在x=1处的切线方程y=$-\frac{1}{2}$,
(Ⅱ)f′(x)=$\frac{1}{x}$-x,令f′(x)=0,
得x=1,
当0<x<1时,f′(x)>0,f(x)单调递增,
x>1时,f′(x)<0,f(x)单调递减,
f(x)的单调递增区间为[1,+∞),
f(x)的单调递减区间为(0,1);
(Ⅲ)证明:h(x)=af(x)+(a+1)g(x)=$\frac{{x}^{2}}{2}$+alnx-(a+1)x,(x>0)
∴h′(x)=x-(a+1)+$\frac{a}{x}$≥2$\sqrt{a}$-(a+1),
当且仅当x=$\frac{a}{x}$,x=$\sqrt{a}$,
设g(x)=2$\sqrt{a}$-(a+1)
g′(x)=$\frac{1}{\sqrt{a}}-1$,0<a≤1,g′(x)>0,g(x)单调递增,当a=1取最大值,最大值为0,
∴h′(x)>0,
∴h(x)单调递增,
h(a)=$-\frac{{a}^{2}}{2}-a+alna$0<a≤1
∴h(a)<0,
当x>1时,h(x)>0,利用零点定理,
∴函数h(x)仅有一个零点.
点评 本题考查根据导数求函数的切线方程和单调区间及判断函数的零点,属于中档题.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:选择题
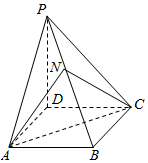 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:6 | D. | 1:8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,E是BC的中点,现沿AD将平面PAD折起,使得PA⊥AB;
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,E是BC的中点,现沿AD将平面PAD折起,使得PA⊥AB;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | -23 | C. | -5或$\frac{5}{2}$ | D. | 5或-$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com