
分析 (1)由题意画出几何体的直观图,进一步得到三视图;
(2)求出一个侧面正三角形的面积,乘以8求得几何体的侧面积,然后求出上部分正三棱锥的高,求得四棱锥的体积,乘以2得答案.
解答 解:(1)该几何体的三视图与直观图如图所示,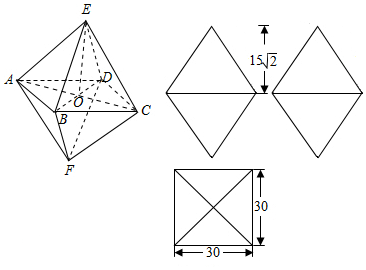
(2)这个是一个正八面体,假设另两个顶点为E,F,
ABCD是正方形,边长=30cm,
每个三角形面积是$\frac{1}{2}×30×15\sqrt{3}=225\sqrt{3}$,则表面积S=8×225$\sqrt{3}=2000\sqrt{3}$(cm2);
体积可以分成两部分,两部分是对称的四棱锥,连接AC,BD交于O,连接EO,
EO就是所要求的高,EO=15$\sqrt{2}$(cm),
半部分四棱锥体积是$\frac{1}{3}×30×30×15\sqrt{2}=4500\sqrt{2}$(cm3),总体积=9000$\sqrt{2}$(cm3).
点评 本题考查柱、锥、台体的体积,考查空间几何体的三视图和直观图,考查空间想象能力和思维能力,是中档题.


科目:高中数学 来源: 题型:解答题
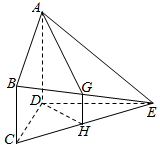 已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.
已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
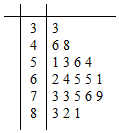 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
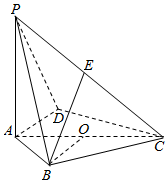 如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB
如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com