
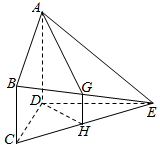
 已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.
已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.分析 (1)由平面ABCD⊥平面CDE得BC⊥平面CDE,由中位线定理得GH∥BC,故GH⊥平面CDE,于是GH⊥CE,由CD=DE得DH⊥CE,故而CE⊥平面ADHG,从而得出AG⊥CE;
(2)多面体ABG-DCH的体积对于四棱锥E-ABCD的体积减去四棱锥E-ADHG的体积.
解答 (1)证明:∵CD=DE,H是CE的中点,
∴DH⊥CE.
∵平面ABCD⊥平面CDE,平面ABCD∩平面CDE=CD,BC⊥CD,BC?平面ABCD,
∴BC⊥平面CDE,
∵G,H分别是BE,CE的中点,
∴HG∥BC,
∴GH⊥平面CDE,∵CE?平面CDE,
∴GH⊥CE,
又DH?平面ADHG,GH?平面ADHG,DH∩HG=H,
∴CE⊥平面ADHG,∵AG?平面ADHG,
∴AG⊥CE.
(2)解:∵BC⊥平面CDE,BC∥AD,
∴AD⊥平面CDE,∵DE?平面CDE,
∴AD⊥DE,又CD⊥DE,CD?平面ABCD,AD?平面ABCD,AD∩CD=D,
∴DE⊥平面ABCD,
∴VE-ABCD=$\frac{1}{3}{S}_{梯形ABCD}•DE$=$\frac{1}{3}×\frac{1}{2}×$(1+2)×2×2=2.
∵GH是△BCE的中位线,
∴GH=$\frac{1}{2}BC$=$\frac{1}{2}$.
∵AD⊥平面CDE,DH?平面CDE,
∴AD⊥DH,∴四边形ADHG是梯形.
∵DC=DE=2,DC⊥DE,H是CE中点,∴CE=2$\sqrt{2}$,DH=HE=$\frac{1}{2}CE$=$\sqrt{2}$.
∴VE-ADHG=$\frac{1}{3}{S}_{梯形ADHG}•EH$=$\frac{1}{3}×\frac{1}{2}×(2+\frac{1}{2})×\sqrt{2}×\sqrt{2}$=$\frac{5}{6}$.
∴多面体ABG-DCH的体积V=VE-ABCD-VE-ADHG=$\frac{7}{6}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥S-ABCD,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,E为线段AD的中点.
如图,已知四棱锥S-ABCD,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,E为线段AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
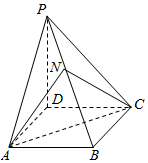 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:6 | D. | 1:8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
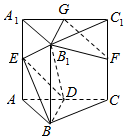 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com