
| A. | 当b=0时,数列{an}是等差数列 | B. | 当b≠0时,数列{an}是等比数列 | ||
| C. | 当b=0时,Sn=a1 | D. | 当b≠0时,Sn=$\frac{{{a_1}({1-{b^n}})}}{1-b}$ |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60)内适合投掷相关方面训练,试估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60)内适合投掷相关方面训练,试估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )| A. | 4:3:1 | B. | 5:3:1 | C. | 5:3:2 | D. | 3:2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
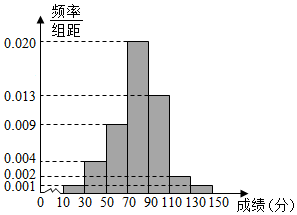 某高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
某高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 23 | B. | 19 | C. | -17 | D. | -18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com