
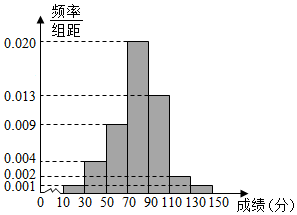
 某高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
某高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.分析 (1)设这100名学生参加初赛成绩的中位数为x,由频率分布直方图的性质能求出这100名学生参加初赛成绩的中位数.
(2)由频率分布直方图得该校初赛分数在[110,130)的人数为4人,分数在[130,150]的人数为2人,由此能求出选取的三人的初赛成绩在频率分布直方图中处于同组的概率.
解答 解:(1)设这100名学生参加初赛成绩的中位数为x,
由频率分布直方图,得:
(0.001+0.004+0.009)×20+0.02×(x-70)=0.5,
解得x=81.
∴这100名学生参加初赛成绩的中位数为81.
(2)由频率分布直方图得该校初赛分数在[110,130)的人数为:0.002×20×100=4人,
分数在[130,150]的人数为0.001×20×100=2人,
该校推荐初赛成绩在110分以上的学生代表学校参加竞赛,在该校推荐参加竞赛的学生中随机抽取3人,
基本事件总数n=${C}_{6}^{3}$=20,
选取的三人的初赛成绩在频率分布直方图中处于同组包含的基本事件个数m=${C}_{4}^{3}$=4,
∴选取的三人的初赛成绩在频率分布直方图中处于同组的概率p=$\frac{m}{n}$=$\frac{4}{20}=\frac{1}{5}$.
点评 本题考查中位数和概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{26}$ | B. | $\sqrt{26}$-1 | C. | $\sqrt{26}$+1 | D. | $\sqrt{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{27}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当b=0时,数列{an}是等差数列 | B. | 当b≠0时,数列{an}是等比数列 | ||
| C. | 当b=0时,Sn=a1 | D. | 当b≠0时,Sn=$\frac{{{a_1}({1-{b^n}})}}{1-b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 13 | C. | $\sqrt{13}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com