
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 联立椭圆方程和直线方程,求得A,B两点的纵坐标,把|AF|=3|FB|化为纵坐标的关系得答案.
解答 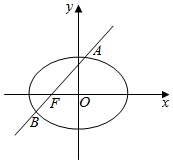 解:如图,
解:如图,
联立$\left\{\begin{array}{l}{y=x+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,得(a2+b2)y2-2b2cy-b4=0.
解得:$y=\frac{2{b}^{2}c±\sqrt{(-2{b}^{2}c)^{2}-4({a}^{2}+{b}^{2})×(-{b}^{4})}}{2({a}^{2}+{b}^{2})}$=$\frac{2{b}^{2}c±\sqrt{8{a}^{2}{b}^{4}}}{2({a}^{2}+{b}^{2})}$,
即${y}_{B}=\frac{{b}^{2}c-\sqrt{2}a{b}^{2}}{{a}^{2}+{b}^{2}}$,${y}_{A}=\frac{{b}^{2}c+\sqrt{2}a{b}^{2}}{{a}^{2}+{b}^{2}}$.
∵|AF|=3|FB|,∴yA=-3yB,
则$\frac{{b}^{2}c+\sqrt{2}a{b}^{2}}{{a}^{2}+{b}^{2}}=-3\frac{{b}^{2}c-\sqrt{2}a{b}^{2}}{{a}^{2}+{b}^{2}}$,
∴${b}^{2}c+\sqrt{2}a{b}^{2}=-3{b}^{2}c+3\sqrt{2}a{b}^{2}$,
即$4{b}^{2}c=2\sqrt{2}a{b}^{2}$,
∴$a=\sqrt{2}c$,
∴$\frac{c}{a}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查了椭圆的简单几何性质,考查了直线与圆锥曲线的关系,运用了数学转化思想方法,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
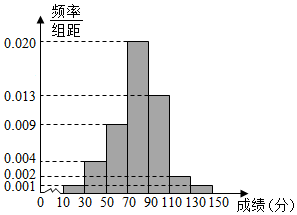 某高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
某高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
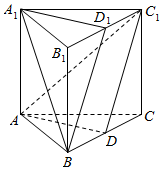 如图所示,正三棱柱ABC-A1B1C1中,A1A=3,AB=2,D是BC上的中点,D1是B1C1的中点,
如图所示,正三棱柱ABC-A1B1C1中,A1A=3,AB=2,D是BC上的中点,D1是B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
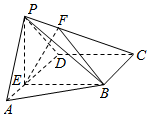 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抛物线 | B. | 椭圆 | C. | 双曲线的右支 | D. | 一条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com