
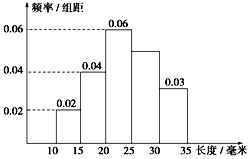
 ��һ������ij��ȣ���λ��mm�����г�����⣬�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����ݱ����������������[20��25���ϵ�Ϊһ��Ʒ��������[15��20��������[25��30���ϵ�Ϊ����Ʒ��������[10��15����[30��35���ϵ�Ϊ����Ʒ��
��һ������ij��ȣ���λ��mm�����г�����⣬�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����ݱ����������������[20��25���ϵ�Ϊһ��Ʒ��������[15��20��������[25��30���ϵ�Ϊ����Ʒ��������[10��15����[30��35���ϵ�Ϊ����Ʒ������ ������Ƶ�ʷֲ�ֱ��ͼ�ɵò�Ʒ�����ڸ����е�Ƶ�ʣ���Ƶ�ʹ��Ƴ���������Ʒ�������ȡһ������Ϊ����Ʒ�ĸ��ʣ�
�����оٳ�һ�п��ܵĽ����ɵĻ����¼���ǡ��1���ij���������[30��35���ϵĻ����¼���6�������ùŵ���͵ĸ��ʹ�ʽ������ʣ�
��� �⣺������Ƶ�ʷֲ�ֱ��ͼ�ɵò�Ʒ������[10��15��Ƶ��Ϊ0.1����[15��20��Ƶ��Ϊ0.2��
[20��25��֮���Ƶ��Ϊ0.3����[30��35��Ƶ��Ϊ0.15��������[25��30���ϵ�Ƶ��Ϊ0.25��
���������ж���Ʒ��Ƶ��Ϊ0.45�����Ը�����Ʒ�������ȡһ��������Ϊ����Ʒ��
����0.45����..��6�֣�
������Ϊһ��Ʒ6����������[10��15����2������[30��35����3������[10��15����2��Ϊa1��a2����[30��35����3��b1��b2��b3������һ�п��ܵĽ����ɵĻ����¼��ռ�
��={��a1��a2������a1��b1������a1��b2������a1��b3����}��15�������¼���ɣ�
ǡ��1���ij���������[30��35���ϵĻ����¼���6����
����ȡ����������Ʒ��ǡ��1���ij���������[30��35���ϵĸ���P=$\frac{2}{5}$����..��12�֣�
���� ���⿼��Ƶ�ʷֲ�����Ƶ�ʷֲ�ͼ����Ƶ�ʹ��Ƹ��ʵ�֪ʶ���������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
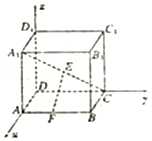 ��ͼ��ʾ���ڿռ�ֱ������ϵ�У�D������ԭ�㣬��һ�ⳤΪa��������ABCD-A1B1C1D1��E��F�ֱ�����Խ���A1C����AB�ϵĶ��㣬��|EF|����СֵΪ��������
��ͼ��ʾ���ڿռ�ֱ������ϵ�У�D������ԭ�㣬��һ�ⳤΪa��������ABCD-A1B1C1D1��E��F�ֱ�����Խ���A1C����AB�ϵĶ��㣬��|EF|����СֵΪ��������| A�� | $\sqrt{2}a$ | B�� | $\frac{{\sqrt{2}}}{2}a$ | C�� | a | D�� | $\frac{1}{2}a$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
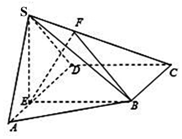 ��ͼ��������S-ABCD�У�ƽ��SAD�͵���ABCD��$��SAD=\frac{��}{3}$����AD����ȡһ��E��ʹ��BCDEΪ���Σ�SA=2AE=DE=2��
��ͼ��������S-ABCD�У�ƽ��SAD�͵���ABCD��$��SAD=\frac{��}{3}$����AD����ȡһ��E��ʹ��BCDEΪ���Σ�SA=2AE=DE=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | $\sqrt{3}$ | D�� | $\sqrt{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com