
【题目】已知函数![]() ,其中
,其中![]() ,
, ![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调减区间;
的单调减区间;
(3)若![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)当
(2)当![]() 时,
时, ![]() 无单调减区间;当
无单调减区间;当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() ;当
;当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() .(3)
.(3)![]()
【解析】试题分析:(1)先对函数解析式进行求导,再借助导数的几何意义求出切线的斜率,运用点斜式求出切线方程;(2)先对函数的解析式进行求导,然后借助导函数的值的符号与函数单调性之间的关系进行分类分析探求;(3)先不等式![]() 进行等价转化,然后运用导数知识及分类整合的数学思想探求函数的极值与最值,进而分析推证不等式的成立求出参数的取值范围。
进行等价转化,然后运用导数知识及分类整合的数学思想探求函数的极值与最值,进而分析推证不等式的成立求出参数的取值范围。
解:(1)因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以切线方程为![]() .
.
(2) 因为![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 无单调减区间.
无单调减区间.
当![]() 即
即![]() 时,列表如下:
时,列表如下:

所以![]() 的单调减区间是
的单调减区间是![]() .
.
当![]() 即
即![]() 时,
时, ![]() ,列表如下:
,列表如下:
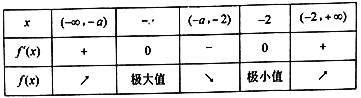
所以![]() 的单调减区间是
的单调减区间是![]() .
.
综上,当![]() 时,
时, ![]() 无单调减区间;
无单调减区间;
当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() ;
;
当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() .
.
(3) ![]() .
.
当![]() 时,由(2)可得,
时,由(2)可得, ![]() 为
为![]() 上单调增函数,
上单调增函数,
所以![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ,符合题意.
,符合题意.
当![]() 时,由(2)可得,要使
时,由(2)可得,要使![]() 在区间
在区间![]() 上恒成立,
上恒成立,
只需![]() ,
, ![]() ,解得
,解得![]() .
.
当![]() 时,可得
时,可得![]() ,
, ![]() .
.
设![]() ,则
,则![]() ,列表如下:
,列表如下:

所以![]() ,可得
,可得![]() 恒成立,所以
恒成立,所以![]() .
.
当![]() 时,可得
时,可得![]() ,无解.
,无解.
综上, ![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,B1 C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程。
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]()
![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]()
试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com