
分析 (Ⅰ)设插入的两个数分别为a,b,结合已知求得公差,再由等差数列的定义求得a,b;
(Ⅱ)设在96与3中间插入4个数分别为a,b,c,d,由等比数列的通项公式求得公比,再由等比数列的定义求得四个数.
解答 解:(Ⅰ)设插入的两个数分别为a,b,则8,a,b,215成等差数列,
设公差为d,则$d=\frac{215-8}{4-1}=69$,
∴a=8+69=77,b=77+69=146.
故两个数为77,146;
(Ⅱ)设在96与3中间插入4个数分别为a,b,c,d,
则96,a,b,c,d,3成等比数列,设公比为q,
∴$q=\root{5}{\frac{3}{96}}=\root{5}{\frac{1}{32}}=\frac{1}{2}$,
∴$a=96×\frac{1}{2}=48$,b=$48×\frac{1}{2}=24$,c=$24×\frac{1}{2}=12$,d=$12×\frac{1}{2}=6$.
故四个数为48,24,12,6.
点评 本题是等差数列与等比数列的综合题,考查了等差数列与等比数列的性质,是中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:填空题
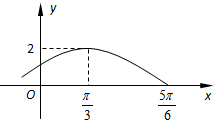 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.则函数y=f(x)的解析式为$f(x)=2sin(x+\frac{π}{6})$.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.则函数y=f(x)的解析式为$f(x)=2sin(x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-e | B. | e-1 | C. | -1-e | D. | e+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
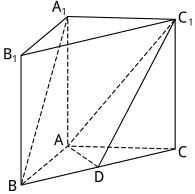 如图,在直三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,D是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com