
| A. | (-∞,-1-$\sqrt{10}$) | B. | $(-1-\sqrt{10},-1+\sqrt{10})$ | C. | $[{-1+\sqrt{10},+∞})$ | D. | $[{-1-\sqrt{10},-1+\sqrt{10}}]$ |
分析 先把2x+y转化为2x+y=(2x+y)($\frac{2}{x}+\frac{1}{y}$)展开后利用基本不等式求得其最小值,然后根据2x+y>m2+2m恒成立求得m2+2m<9,进而求得m的范围.
解答 解:∵x>0,y>0,$\frac{2}{x}+\frac{1}{y}$=1,
∴2x+y=(2x+y)($\frac{2}{x}+\frac{1}{y}$)=4+1+$\frac{2y}{x}$+$\frac{2x}{y}$≥5+2$\sqrt{\frac{2y}{x}•\frac{2x}{y}}$=9,
当且仅当x=y=3时取等号,
∵2x+y>m2+2m恒成立,
∴m2+2m<9,
解得-1-$\sqrt{10}$<x<-1+$\sqrt{10}$,
故选:B.
点评 本题主要考查了基本不等式在最值问题中的应用.考查了学生分析问题和解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
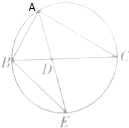 如图,在Rt△ABC中,直角A的角平分线AD的延长线交它的外接圆于点E,AD=1.6,AE=3.
如图,在Rt△ABC中,直角A的角平分线AD的延长线交它的外接圆于点E,AD=1.6,AE=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{12}$单位 | B. | 向左平移$\frac{π}{6}$单位 | C. | 向右平移$\frac{π}{12}$单位 | D. | 向右平移$\frac{π}{6}$单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x3+x5<2x4 | B. | x3+x5=2x4 | C. | x3+x5>2x4 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com