
| y1 | y2 | |
| x1 | 10 | 18 |
| x2 | m | 26 |
| A. | 8 | B. | 9 | C. | 14 | D. | 19 |
分析 根据题意,由独立性检验的性质,当|ad-bc|越大,两个变量有关的可能性就越大,依次计算四个选项中|ad-bc|的值,比较可得答案.
解答 解:根据题意,依次分析选项:
对于A、|ad-bc|=|10×26-18×m|=10×26-18×8=116,
对于B、|ad-bc|=|10×26-18×m|=10×26-18×9=98,
对于C、|ad-bc|=|10×26-18×m|=10×26-18×14=8,
对于D、|ad-bc|=|10×26-18×m|=|10×26-18×19|=82,
比较可得:当m=14时,|ad-bc|的值最小,故X与Y的关系最弱;
故选:C.
点评 本题考查独立性检验,|ad-bc|越大,两个变量有关的可能性就越大是解决问题的关键,属基础题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | 2x+3y-12=0 | B. | 2x+3y+12=0 | C. | 2x-3y+12=0 | D. | 2x-3y-12=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一或第二象限 | B. | 第二或第三象限 | C. | 第一或第三象限 | D. | 第二或第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
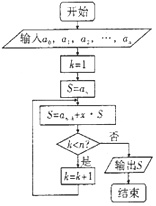 秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )
秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )| A. | 248 | B. | 258 | C. | 268 | D. | 278 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com