
分析 (1)由已知利用三角函数恒等变换的应用化简可得f(x)=sin(2x-$\frac{π}{6}$)-1,结合x的范围,可求$2x-\frac{π}{6}∈[-\frac{π}{6},\frac{5π}{6}]$,利用正弦函数的性质可求函数y=f(x)在[0,$\frac{π}{2}$]上的最大值和最小值.
(2)由已知可求sin(2B-$\frac{π}{6}$)=1,结合B的范围,可求2B-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{11π}{6}$),可求B的值,利用余弦定理可求AC的值,进而利用正弦定理即可得解sinA的值.
解答 解:(1)∵$f(x)=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cosx-1=sin(2x-\frac{π}{6})-1$,
∵$x∈[0,\frac{π}{2}]$,
∴$2x-\frac{π}{6}∈[-\frac{π}{6},\frac{5π}{6}]$,
∴$sin(2x-\frac{π}{6})∈[-\frac{1}{2},1]$,
∴$f(x)∈[-\frac{3}{2},0]$,
∴y=f(x)的最大值为0,最小值为$-\frac{3}{2}$.
(2)∵f(B)=0,即sin(2B-$\frac{π}{6}$)=1,
又∵B∈(0,π),2B-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{11π}{6}$),
∴2B-$\frac{π}{6}$=$\frac{π}{2}$,可得:B=$\frac{π}{3}$,
又∵在△ABC中,由余弦定理可得:b2=a2+c2-2accos$\frac{π}{3}$=4+9-2×$2×3×\frac{1}{2}$=7,
∴AC=$\sqrt{7}$,
∵由正弦定理得:$\frac{b}{sinB}=\frac{a}{sinA}$,即$\frac{{\sqrt{7}}}{{sin\frac{π}{3}}}=\frac{3}{sinA}$,
∴$sinA=\frac{{3\sqrt{21}}}{14}$.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的性质,余弦定理,正弦定理在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 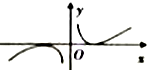 | ||
| C. | 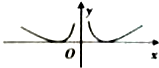 | D. | 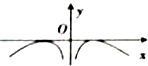 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>f(2) | B. | f(1)<f(2) | ||
| C. | f(1)=f(2) | D. | f(1)与f(2)大小无法判定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com