Question

8£®ÈôµÈ±ßÈý½ÇÐÎABCµÄ±ß³¤Îª2£¬NΪABµÄÖе㣬ÇÒABÉÏÒ»µãMÂú×ã$\overrightarrow{CM}$=x$\overrightarrow{CA}$+y$\overrightarrow{CB}$£¬Ôòµ±$\frac{1}{x}$+$\frac{4}{y}$È¡×îСֵʱ£¬$\overrightarrow{CM}$•$\overrightarrow{CN}$=£¨¡¡¡¡£©

• A£® 6
• B£® 5
• C£® 4
• D£® 3

Answer 1

·ÖÎö ¿É»­³öͼÐΣ¬²¢ÓÉÌõ¼þ¿ÉÖªx£¾0£¬y£¾0£¬²¢¿ÉµÃ³öx+y=1£¬´Ó¶øµÃµ½$\frac{1}{x}+\frac{4}{y}=\frac{x+y}{x}+\frac{4£¨x+y£©}{y}$£¬ÓÉ»ù±¾²»µÈʽ±ã¿ÉµÃ³ö$\frac{1}{x}+\frac{4}{y}$µÄ×îСֵ£¬ÒÔ¼°¶ÔÓ¦µÄx£¬yÖµ£¬´Ó¶øÓÃ$\overrightarrow{CA}£¬\overrightarrow{CB}$±íʾ³ö$\overrightarrow{CM}$£¬¶ø$\overrightarrow{CN}=\frac{1}{2}£¨\overrightarrow{CA}+\overrightarrow{CB}£©$£¬ÕâÑù¸ù¾Ý¡÷ABCΪµÈ±ßÈý½ÇÐμ´¿É½øÐÐÏòÁ¿ÊýÁ¿»ýµÄÔËË㣬´Ó¶øÇó³ö$\overrightarrow{CM}•\overrightarrow{CN}$µÄÖµ£®

½â´ð ½â£ºÈçͼ£¬¿ÉÖª£¬x£¾0£¬y£¾0£»

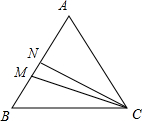
¡ßM£¬A£¬BÈýµã¹²Ïߣ¬ÇÒ$\overrightarrow{CM}=x\overrightarrow{CA}+y\overrightarrow{CB}$£»
¡àx+y=1£»
¡à$\frac{1}{x}+\frac{4}{y}=\frac{x+y}{x}+\frac{4£¨x+y£©}{y}$
=$1+\frac{y}{x}+\frac{4x}{y}+4$
¡Ý1+4+4£¬µ±$\frac{y}{x}=\frac{4x}{y}$£¬¼´y=2xʱȡ¡°=¡±£¬¼´$\frac{1}{x}+\frac{4}{y}$È¡×îСֵ£»
´Ëʱx=$\frac{1}{3}$£¬$y=\frac{2}{3}$£»
¡ßNÊÇABµÄÖе㣻
¡à$\overrightarrow{CM}•\overrightarrow{CN}=£¨\frac{1}{3}\overrightarrow{CA}+\frac{2}{3}\overrightarrow{CB}£©•$$[\frac{1}{2}£¨\overrightarrow{CA}+\overrightarrow{CB}£©]$
=$\frac{1}{2}£¨\frac{1}{3}{\overrightarrow{CA}}^{2}+\overrightarrow{CA}•\overrightarrow{CB}+\frac{2}{3}{\overrightarrow{CB}}^{2}£©$
=$\frac{1}{2}£¨\frac{4}{3}+2+\frac{8}{3}£©$
=3£®
¹ÊÑ¡£ºD£®

µãÆÀ ¿¼²éÏòÁ¿¼Ó·¨µÄƽÐÐËıßÐη¨Ôò£¬ÈýµãA£¬B£¬C¹²ÏߵijäÒªÌõ¼þ£º$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$£¬ÇÒx+y=1£¬»ù±¾²»µÈʽµÄÔËÓã¬×¢Òâ»ù±¾²»µÈʽµÈºÅ³ÉÁ¢µÄÌõ¼þ£¬ÏòÁ¿ÊýÁ¿»ýµÄÔËËã¼°¼ÆË㹫ʽ£®