
【题目】设函数![]() .
.
(1)若![]() ,证明:
,证明: ![]() 在
在![]() 上存在唯一零点;
上存在唯一零点;
(2)设函数![]() ,(
,( ![]() 表示
表示![]() 中的较小值),若
中的较小值),若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)证明![]() 在
在![]() 上存在唯一零点,需从两个方面进行,一是单调性,确保至多一个零点,二是零点存在定理,确保至少一个零点.(2)即求函数
上存在唯一零点,需从两个方面进行,一是单调性,确保至多一个零点,二是零点存在定理,确保至少一个零点.(2)即求函数![]() 的最大值,根据分段函数最大值为各段最大值的最大值,先求各段函数单调性,确定最大值,并比较可得函数最大值.
的最大值,根据分段函数最大值为各段最大值的最大值,先求各段函数单调性,确定最大值,并比较可得函数最大值.
试题解析:
解:(1)函数![]() 的定义域为
的定义域为![]() ,因为
,因为![]() ,当
,当![]() 时,
时, ![]() ,而
,而![]() ,所以
,所以![]() 在
在![]() 存在零点.因为
存在零点.因为![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() ,则
,则![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
(2)由(1)得, ![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,
, ![]() 时,
时, ![]() 时,
时,
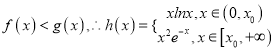 .当
.当![]() 时,由于
时,由于![]() ;
; ![]() 时,
时, ![]() ,于是
,于是![]() 在
在![]() 单调递增,则
单调递增,则![]() ,所以当
,所以当![]() 时,
时, ![]() .当
.当![]() 时,因为
时,因为![]() ,
, ![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 单调递增;
单调递增; ![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 单调递减,于是当
单调递减,于是当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 的最大值为
的最大值为![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=|lnx|,若函数g(x)=f(x)﹣ax在区间(0,3]上有三个零点,则实数a的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,e)
,e)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
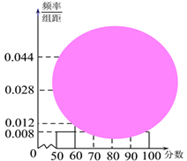
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图:
![]() 求分数在
求分数在![]() 的频率及全班人数;
的频率及全班人数;
![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|mx|﹣|x﹣n|(0<n<1+m),若关于x的不等式f(x)<0的解集中的整数恰有3个,则实数m的取值范围为( )
A.3<m<6
B.1<m<3
C.0<m<1
D.﹣1<m<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
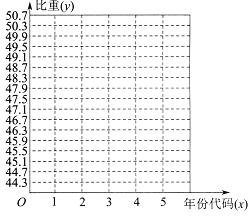
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
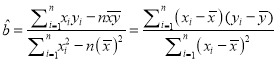 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列各组中两个函数是否为同一函数.
(1)f(x)=x2+2x﹣1,g(x)=t2+2t﹣1;
(2)f(x)=![]() , g(x)=x+1;
, g(x)=x+1;
(3)f(x)=![]()
![]() , g(x)=
, g(x)=![]() ;
;
(4)f(x)=|3﹣x|+1,g(x)=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2lnx﹣a(x2﹣1),a∈R,若当x≥1时,f(x)≥0恒成立,则a的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞,0]
C.(﹣∞,1]
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:
(单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:

设该险种一续保人一年内出险次数与相应概率如下:

(1) 求一续保人本年度的保费高于基本保费的概率;
(2) 若一续保人本年度的保费高于基本保费用,求其保费比基本保费高出60%的概率;
(3) 求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com