
【题目】已知定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2),当x∈[0,2)时,f(x)=﹣2x2+4x.设f(x)在[2n﹣2,2n)上的最大值为an(n∈N*),且{an}的前n项和为Sn , 则Sn=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:∵定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2), ∴f(x+2)= ![]() f(x),
f(x),
∴f(x+4)= ![]() f(x+2)=
f(x+2)= ![]() f(x),f(x+6)=
f(x),f(x+6)= ![]() f(x+4)=
f(x+4)= ![]() f(x),…f(x+2n)=
f(x),…f(x+2n)= ![]() f(x)
f(x)
设x∈[2n﹣2,2n),则x﹣(2n﹣2)∈[0,2)
∵当x∈[0,2)时,f(x)=﹣2x2+4x.
∴f[x﹣(2n﹣2)]=﹣2[(x﹣(2n﹣2)]2+4[x﹣(2n﹣2)].
∴ ![]() =﹣2(x﹣2n+1)2+2
=﹣2(x﹣2n+1)2+2
∴f(x)=21﹣n[﹣2(x﹣2n+1)2+2],x∈[2n﹣2,2n),
∴x=2n﹣1时,f(x)的最大值为22﹣n
∴an=22﹣n
∴{an}表示以2为首项, ![]() 为公比的等比数列
为公比的等比数列
∴{an}的前n项和为Sn= 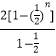 =
= ![]()
故选B.
根据定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2),可得f(x+2)= ![]() f(x),从而f(x+2n)=
f(x),从而f(x+2n)= ![]() f(x),利用当x∈[0,2)时,f(x)=﹣2x2+4x,可求(x)在[2n﹣2,2n)上的解析式,从而可得f(x)在[2n﹣2,2n)上的最大值为an , 进而利用等比数列的求和公式,即可求得{an}的前n项和为Sn .
f(x),利用当x∈[0,2)时,f(x)=﹣2x2+4x,可求(x)在[2n﹣2,2n)上的解析式,从而可得f(x)在[2n﹣2,2n)上的最大值为an , 进而利用等比数列的求和公式,即可求得{an}的前n项和为Sn .


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
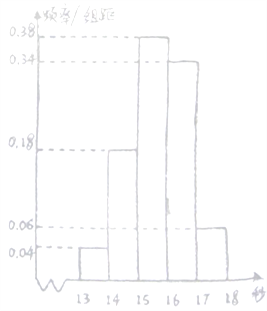
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2,AB=2 ![]() .
. 
(1)求异面直线PC与AD所成角的大小;
(2)若平面ABCD内有一经过点C的曲线E,该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等于PC与AD所成角.试判断曲线E的形状并说明理由;
(3)在平面ABCD内,设点Q是(2)题中的曲线E在直角梯形ABCD内部(包括边界)的一段曲线CG上的动点,其中G为曲线E和DC的交点.以B为圆心,BQ为半径r的圆分别与梯形的边AB、BC交于M、N两点.当Q点在曲线段CG上运动时,试求圆半径r的范围及VP﹣BMN的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一辆赛车在一个周长为![]() 的封闭跑道上行驶,跑道由几段直道和弯道组成,图
的封闭跑道上行驶,跑道由几段直道和弯道组成,图![]() 反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.

图1

图2
根据图![]() 有以下四个说法:
有以下四个说法:
①在这第二圈的![]() 到
到![]() 之间,赛车速度逐渐增加;
之间,赛车速度逐渐增加;
②在整个跑道中,最长的直线路程不超过![]() ;
;
③大约在这第二圈的![]() 到
到![]() 之间,赛车开始了那段最长直线路程的行驶;
之间,赛车开始了那段最长直线路程的行驶;
④在图![]() 的四条曲线(注:
的四条曲线(注:![]() 为初始记录数据位置)中,曲线
为初始记录数据位置)中,曲线![]() 最能符合赛车的运动轨迹.
最能符合赛车的运动轨迹.
其中,所有正确说法的序号是( )
A. ①②③ B. ②③ C. ①④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com