
【题目】【2017河北唐山二模】已知函数![]() 的图象与
的图象与![]() 轴相切,
轴相切,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,求证:
,求证:![]()
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)对函数求导,设![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,由题意可得在该点处导数值为0,函数值为0,构造方程组可得
,由题意可得在该点处导数值为0,函数值为0,构造方程组可得![]() 的值,将题意转化为
的值,将题意转化为![]() ,设
,设![]() ,利用导数判断其单调性求出最大值即可;(Ⅱ)构造函数
,利用导数判断其单调性求出最大值即可;(Ⅱ)构造函数![]() ,对其求导结合(Ⅰ)可得
,对其求导结合(Ⅰ)可得![]() 的单调性,从而有
的单调性,从而有![]() ,化简整理可得
,化简整理可得![]() ,运用换底公式及(Ⅰ)中的不等式
,运用换底公式及(Ⅰ)中的不等式![]() 可得
可得![]()
![]() ,再次运用
,再次运用![]() 可得结论.
可得结论.
试题解析:(Ⅰ)![]() ,设
,设![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,
,
则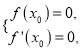 即
即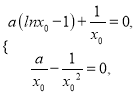
解得![]() .
.
所以![]() ,
,
![]() 等价于
等价于![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() ,
,
即![]() ,(*),所以
,(*),所以![]() .
.
(Ⅱ)设![]() ,则
,则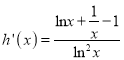 ,
,
由(Ⅰ)可知,当![]() 时,
时,![]() ,
,
从而有![]() ,所以
,所以![]() 单调递增,
单调递增,
又![]() ,所以
,所以![]() ,
,
从而有![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
又![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
综上可知,![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知左焦点为F(﹣1,0)的椭圆过点E(1, ![]() ).过点P(1,1)分别作斜率为k1 , k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1 , k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
(1)求椭圆的标准方程;
(2)若P为线段AB的中点,求k1;
(3)若k1+k2=1,求证直线MN恒过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:①、若m>0,则方程x2﹣x+m=0有实根. ②、若x>1,y>1,则x+y>2的逆命题. ③、对任意的x∈{x|﹣2<x<4},|x﹣2|<3的否定形式. ④、△>0是一元二次方程ax2+bx+c=0有一正根和一负根的充要条件.是真命题的有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式;
(2)求数列{nan}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取![]() 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值![]() ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.
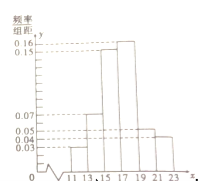
(1)估计该技术指标值![]() 平均数
平均数![]() ;
;
(2)在直方图的技术指标值分组中,以![]() 落入各区间的频率作为
落入各区间的频率作为![]() 取该区间值的频率,若
取该区间值的频率,若![]() ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取![]() 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(x,1);
=(x,1);
(1)若( ![]() +2
+2 ![]() )⊥(2
)⊥(2 ![]() ﹣
﹣ ![]() )时,求x的值;
)时,求x的值;
(2)若向量 ![]() 与向量
与向量 ![]() 的夹角为锐角,求x的取值范围.
的夹角为锐角,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南京一模19】设函数![]() ,
,![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记函数
时,记函数![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式
![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分14分)
在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com