
【题目】数列{an}的前n项和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式;
(2)求数列{nan}的前n项和.
【答案】
(1)解:∵Sn=2an﹣3n,对于任意的正整数都成立,
∴Sn+1=2an+1﹣3n﹣3,
两式相减,得a n+1=2an+1﹣2an﹣3,即an+1=2an+3,
∴an+1+3=2(an+3),
所以数列{bn}是以2为公比的等比数列,
由已知条件得:S1=2a1﹣3,a1=3.
∴首项b1=a1+3=6,公比q=2,
∴an=62n﹣1﹣3=32n﹣3
(2)解:∵nan=3×n2n﹣3n
∴Sn=3(12+222+323+…+n2n)﹣3(1+2+3+…+n),
2Sn=3(122+223+324+…+n2n+1)﹣6(1+2+3+…+n),
∴﹣Sn=3(2+22+23+…+2n﹣n2n+1)+3(1+2+3+…+n)
= ![]()
∴Sn= ![]()
【解析】(1)通过递推关系式求出an与an+1的关系,推出{an+3}即数列{bn}是等比数列,求出数列{bn}的通项公式即可求出{an}的通项公式;(2)写出数列{nan}的通项公式,然后写出前n项和的表达式通过错位相减法求解即可.


科目:高中数学 来源: 题型:
【题目】已知f(x)=log3(1+x)﹣log3(1﹣x).
(1)判断函数f(x)的奇偶性,并加以证明;
(2)已知函数g(x)=log ![]()
![]() ,当x∈[
,当x∈[ ![]() ,
, ![]() ]时,不等式 f(x)≥g(x)有解,求k的取值范围.
]时,不等式 f(x)≥g(x)有解,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 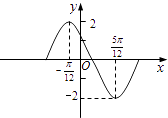
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,圆C:
,圆C: ![]() ,
,
(1)过点![]() 向圆C引切线l,求切线l的方程;
向圆C引切线l,求切线l的方程;
(2)过点A作直线![]() 交圆C于P,Q,且
交圆C于P,Q,且![]() ,求直线
,求直线![]() 的斜率k;
的斜率k;
(3)定点M,N在直线![]() 上,对于圆C上任意一点R都满足
上,对于圆C上任意一点R都满足![]() ,试求M,N两点的坐标.
,试求M,N两点的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
, ![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与
过原点且与![]() 的准线相切.
的准线相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 点![]() ,点
,点![]() (与
(与![]() 不重合)在直线
不重合)在直线![]() 上运动,过点
上运动,过点![]() 作
作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .求证:
.求证: ![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com