【题目】若关于x的不等式（m﹣1）x2﹣mx+m﹣1＞0的解集为空集，则实数m的取值为 ．
【答案】m≤ 
【解析】解：∵关于x的不等式（m﹣1）x2﹣mx+m﹣1＞0的解集为， ∴不等式（m﹣1）x2﹣mx+m﹣1≤0恒成立
①当m﹣1=0时，（m﹣1）x2﹣mx+m﹣1≤0，即x≥0，不是对任意x∈R恒成立；
②当m﹣1≠0时，x∈R，使（m﹣1）x2﹣mx+m﹣1≤0，
即m﹣1＜0且△=（﹣m）2﹣4（m﹣1）（m﹣1）≤0，
解得m≤
综上，实数m的取值范围是m≤ ．
所以答案是m≤ ．
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识，掌握求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．
科目：高中数学 来源： 题型：
【题目】数列{an}的前n项和为Sn ， 若对于任意的正整数n都有Sn=2an﹣3n．
（1）设bn=an+3，求证：数列{bn}是等比数列，并求出{an}的通项公式；
（2）求数列{nan}的前n项和．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
： 
，曲线
： 
（
为参数），以坐标原点
为极点， 
轴正半轴为极轴，建立极坐标系.
（Ⅰ）求曲线
， 
的极坐标方程；
（Ⅱ）曲线
： 
（
为参数， 
， 
）分别交
， 
于
， 
两点，当
取何值时， 
取得最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在
中， 
的中点为
,且
，点
在
的延长线上，且
.固定边
，在平面内移动顶点
，使得圆
与边
，边
的延长线相切，并始终与
的延长线相切于点
，记顶点
的轨迹为曲线
.以
所在直线为
轴， 
为坐标原点如图所示建立平面直角坐标系.
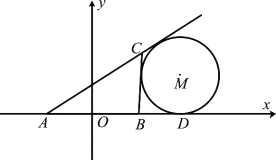
（Ⅰ）求曲线
的方程；
（Ⅱ）设动直线
交曲线
于
两点，且以
为直径的圆经过点
，求
面积的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
，半径为
的圆
与
相切，圆心在
轴上且在直线的上方．
（Ⅰ）求圆的标准方程；
（Ⅱ）过点
的直线与圆交于
两点（
在轴上方），问在轴正半轴上是否存在点
，使得轴平分
？若存在，请求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知： 
、 
、 
是同一平面上的三个向量，其中 =（1，2）．
（1）若| |=2 
，且 ∥ ，求 的坐标．
（2）若| |= 
，且 +2 与2 ﹣ 垂直，求 与 的夹角θ
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a1=3，an=2an﹣1+（t+1）2n+3m+t（t，m∈R，n≥2，n∈N*）
（1）t=0，m=0时，求证： 
是等差数列；
（2）t=﹣1，m= 
是等比数列；
（3）t=0，m=1时，求数列{an}的通项公式和前n项和．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知空间四边形ABCD的两条对角线的长AC=6，BD=8，AC与BD所成的角为30o ， E，F，G，H分别是AB，BC，CD，DA的中点，求四边形EFGH的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com